练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    3．已知关于x的一元二次方程ax2+bx+c=5的一个根是2，且二次函数y=ax2+bx+c的对称轴是直线x=2，则抛物线y=ax2+bx+c的顶点坐标为（2，5）．

    分析 由二次函数y=ax2+bx+c的对称轴是直线x=2，得出顶点横坐标为2，代入函数解析式得出纵坐标ax2+bx+c=5，由此求得顶点坐标即可．

    解答 解：∵二次函数y=ax2+bx+c的对称轴是直线x=2，方程ax2+bx+c=5的一个根是2，
    ∴当x=2时，y=ax2+bx+c=5，
    ∴抛物线的顶点坐标是（2，5）．
    故答案为：（2，5）．

    点评 本题考查的是二次函数的性质，掌握顶点坐标的计算方法是解决问题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    13．△ABC内接于⊙O，已知∠ABC=∠ACB．
    （1）如图（1），求证：AO平分∠BAC；
    （2）如图（2），点D是弧AC上一点，连接BD交AC于点G，连接CD，弦AE交BD于F、交CD于H，并且AE⊥BD，求证：BD+CD=2BF；
    （3）如图（3）在（2）的条件下，BD经过圆心O，连接DE，OG=DH，S△DEH=9$\sqrt{2}$，求OG的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    14．计算：（-1）2017+$\sqrt{9}$+（$\frac{1}{2}$）-2+$\root{3}{-8}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

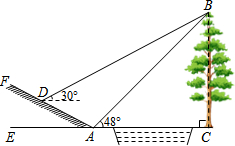    11．如图所示，某中学九年级数学活动小组选定测量学校前面小河对岸大树BC的高度，他们在斜坡上D处测得大树顶端B的仰角是30°，朝大树方向下坡走6米到达坡底A处，在A处测得大树顶端B的仰角是48°．若斜坡FA的坡比i=1：$\sqrt{3}$，求大树的高度．（结果保留一位小数）参考数据：sin48°≈0.74，cos48°≈0.67，tan48°≈1.11，$\sqrt{3}$取1.73．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    18．如图，已知抛物线y=-x2+2x+3与坐标轴交于A，B，C三点，抛物线上的点D与点C关于它的对称轴对称．
    （1）直接写出点D的坐标和直线AD的解析式；
    （2）点E是抛物线上位于直线AD上方的动点，过点E分别作EF∥x轴，EG∥y轴并交直线AD于点F、G，求△EFG周长的最大值；
    （3）若点P为y轴上的动点，则在抛物线上是否存在点Q，使得以A，D，P，Q为顶点的四边形是平行四边形？若存在，请求出点Q的坐标，若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    8．某超市为了吸引顾客，设计了一种促销活动：在一个不透明的箱子里放有4个相同的小球，球面上分别标有“0元”，“10元”，“20元”，“30元”的字样．顾客在该超市一次性消费满200元，就可以在箱子里先后摸出两个小球（每一次摸出后不放回），超市根据两小球上所标金额的和返还等额购物券．若某顾客刚好消费200元，则他所获得购物券的金额不低于30元的概率为$\frac{2}{3}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    15．如图1，在平面直角坐标系中，直线y=-x+1与抛物线y=ax2+bx+c（a≠0）相交于点A（1，0）和点D（-4，5），并与y轴交于点C，抛物线的对称轴为直线x=-1，且抛物线与x轴交于另一点B．
    （1）求该抛物线的函数表达式；
    （2）若点E是直线下方抛物线上的一个动点，求出△ACE面积的最大值；
    （3）如图2，若点M是直线x=-1的一点，点N在抛物线上，以点A，D，M，N为顶点的四边形能否成为平行四边形？若能，请直接写出点M的坐标；若不能，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    12．A城有肥料200t，B城有肥料300t．现要把这些肥料全部运往C，D两乡，从A城往C，D两乡运肥料的费用分别为20元/t和25元/t；从B城往C，D两乡运肥料的费用分别为15元/t和24圆/t．现C乡需要肥料240t，D乡需要肥料260t．设从A城调往C乡肥料xt．
    （1）根据题意，填写下表：
                           调入地
                   水量/万吨
    调出地    		CD
    Ax200-x
    B240-x60+x
    总计240260
    （2）设调运肥料的总运费y（单位：元）是x的函数，求y与x的函数解析式；
    （3）请根据（2）给出完成调运任务总费用最少的调运方案，并说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    13．方程12-x=2x的解是x=4．

    查看答案和解析>>

    同步练习册答案