
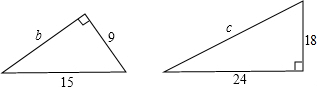
 求图中直角三角形中未知的长度:b=
求图中直角三角形中未知的长度:b=科目:初中数学 来源: 题型:
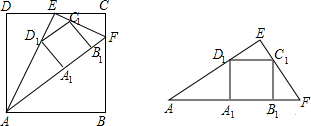
查看答案和解析>>
科目:初中数学 来源:非常讲解·教材全解全析数学八年级上(配课标北师大版) 课标北师大版 题型:044
如图1,在边长为4的正方形ABCD中,E是DC的中点,点F在BC边上,且CF=1,在△AEF中作正方形A1B1C1D1,使边A1B1在AF上,其余两个顶点C1、D1分别在EF和AE上.

(1)请直接写出图中两直角边之比等于1∶2的三个直角三角形(不另添加字母及辅助线);
(2)求AF的长及正方形A1B1C1D1的边长;
(3)在(2)的条件下,取出△AEF,如图2将△EC1D1沿直线C1D1、△C1FB1沿直线C1B1分别向正方形A1B1C1D1内折叠,求小正方形A1B1C1D1未被两个折叠三角形覆盖的四边形面积.
查看答案和解析>>
科目:初中数学 来源:2004年全国中考数学试题汇编《图形的对称》(04)(解析版) 题型:解答题

查看答案和解析>>
科目:初中数学 来源:2004年全国中考数学试题汇编《三角形》(11)(解析版) 题型:解答题

查看答案和解析>>
科目:初中数学 来源:2004年福建省福州市中考数学试卷(解析版) 题型:解答题
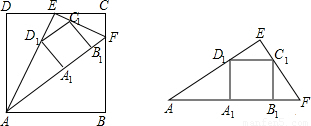
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com