
����Ŀ��ij����������һ�ֲ�Ʒ,���ֲ�Ʒ�ijɱ���Ϊ10Ԫ/ǧ��,��֪���ۼ۲����ڳɱ���,����۲��Ź涨���ֲ�Ʒ�����ۼ۲�����18Ԫ/ǧ��,�г����鷢��,�ò�Ʒÿ���������y(ǧ��)�����ۼ�x(Ԫ/ǧ��)֮��ĺ�����ϵ��ͼ��ʾ:
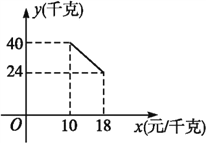
��1����y��x֮��ĺ�����ϵʽ,��д���Ա���x��ȡֵ��Χ;
��2����ÿ�����������W(Ԫ)�����ۼ�x(Ԫ/ǧ��)֮��ĺ�����ϵʽ.�����ۼ�Ϊ����ʱ,ÿ��������������?��������Ƕ���?
��3���þ�������Ҫÿ����168Ԫ����������,���ۼ�Ӧ��Ϊ����?
���𰸡���1��y��x֮��ĺ�����ϵʽy=-2x+60(10��x��18)����2�������ۼ�Ϊ18Ԫʱ,ÿ��������������,���������192Ԫ����3���þ�������Ҫÿ����168Ԫ����������,���ۼ�Ӧ��Ϊ16Ԫ.
����������1���������⣬��һ�κ����Ľ���ʽΪy=kx+b������ͼ�е�������֪�ĵ������(10��40)��(18��24)��������Ԫ�����Ԫһ�η�����ó�k��b��ֵ�����ɵó�һ�κ����Ľ���ʽ��
��2���������������һ�������������������Եõ�W����x�ı���ʽ,Ȼ����ݶ��κ�����������⼴��.
��3����168������κ����Ĺ�ϵʽ����һԪ���η��̼��ɣ�ע���Ա���x��ȡֵ��Χ��
��1����y��x֮��ĺ�����ϵʽy=kx+b,��(10,40),(18,24)�����
![]() , ���
, ���![]() ,
,
��y��x֮��ĺ�����ϵʽy=-2x+60(10��x��18);
��2��W=(x-10)(-2x+60)=-2x2+80x-600,
�Գ���x=20,�ڶԳ�������y����x�����������,
��10��x��18,����x=18ʱ,W���,���Ϊ192.
�������ۼ�Ϊ18Ԫʱ,ÿ��������������,���������192Ԫ
��3����168=-2x2+80x-600,
���x1=16,x2=24(��������,��ȥ)
��:�þ�������Ҫÿ����168Ԫ����������,���ۼ�Ӧ��Ϊ16Ԫ.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ij�ط��������������50km��A��B��վ֮��Ĺ�·��E�㣬��һ�����ز��ӹ����أ���ʹC��D���嵽E��ľ�����ȣ���֪DA��AB��A��CB��AB��B��DA=30km��CB=20km����ô����EӦ������Aվ����ǧ�ĵط���

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ס����������500km��һ�п쳵�Ӽ�ʻ�����أ�;�о����ҵأ�һ���������ҵ�ʻ�����أ�����ͬʱ������ͬ����У�����ABCD��ʾ����֮��ľ���y(km)��������ʻ��ʱ��Ϊx(h)֮��ĺ�����ϵ������ͼ���ṩ����Ϣ������˵������ȷ����(����)
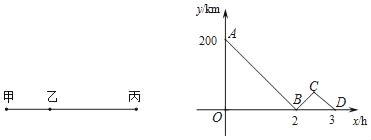
A. �ס�������֮��ľ���Ϊ200 kmB. �쳵�Ӽ�ʻ�����ع�����2.5 h
C. �쳵�ٶ��������ٶȵ�1.5��D. �쳵�������ʱ����������ػ���50 km
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����Ҫ��ͼ����1����ͼ1ƽ�����������![]() ��������Ҫ��ͼ��.
��������Ҫ��ͼ��.
������![]() ��
��
�ڻ�ֱ��![]() ��
��![]() �ڵ�
�ڵ�![]() ��
��
�ۻ����߶�![]() �ķ����ӳ��ߣ�
�ķ����ӳ��ߣ�
������ֱ��![]() ��ȷ��һ��
��ȷ��һ��![]() ��ʹ
��ʹ![]() ���㵽��
���㵽��![]() �ľ���֮����С����д����ͼ������.
�ľ���֮����С����д����ͼ������.
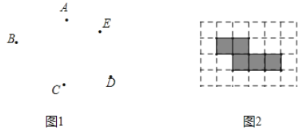
��2����5����Сһ�����������Ƴ���ͼ2��ʾ��ƴ��ͼ�Σ���Ӱ���֣���������ͼ�е�ƴ��ͼ�����ٽ�һ�������Σ�ʹ��ƴ�ӳɵ�ͼ�ξ����۵����ܳ�Ϊһ����յ����������.��ע�⣺ֻ������һ������Ҫ��������Σ�������Ӱ��ʾ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУѧ����ѧ��ȤС��Ϊ�˽ⱾУͬѧ���Ͽ��ⲹϰ���̬�ȣ���ѧУ��ȡ�˲���ͬѧ�������ʾ����飬����ֱ�Ϊ��A���dz���ͬ������B����ͬ������C������ν������D������ͬ��������̬�ȣ��ֽ�����ͳ�ƽ���Ƴ�����ͼ����ͳ��ͼ����������ͳ��ͼ���ش��������⣺
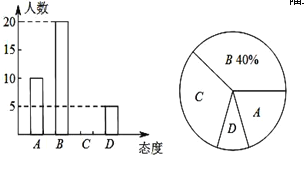
��1����ȡ�˶�����ͬѧ�������ʾ�������
��2���벹ȫ����ͳ��ͼ��
��3���֡�����ͬ��̬�ȵ�ѧ�������İٷֱ���ռ���ε�Բ�Ľ�Ϊ�� ���ȣ�
��4������У��3000��ѧ����������Ƹ�Уѧ���Գ֡���ͬ���͡��dz���ͬ������̬�ȵ�����֮�ͣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
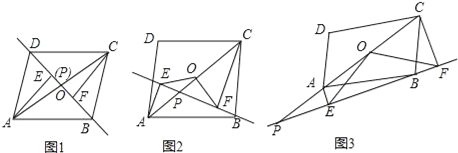
����Ŀ����֪����P��ƽ���ı���ABCD�Խ���AC����ֱ���ϵ�һ�����㣨��P�����A��C�غϣ����ֱ����A��C��ֱ��BP�����ߣ�����ֱ�Ϊ��E��F����OΪAC���е㣮��1������P���O�غ�ʱ��ͼ1����֤OE=OF������֤����
��2��ֱ��BP�Ƶ�B��ʱ�뷽����ת������OFE=30��ʱ����ͼ2��ͼ3��λ�ã������߶�CF��AE��OE֮����������������ϵ����д�����ͼ2��ͼ3�IJ��룬��ѡ��һ���������֤����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC�У�AB=AC����A=40O���ӳ�AC��D��ʹCD=BC����P����ABD�����ģ����BPC=

A. 105�� B. 110�� C. 130�� D. 145��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��ͼ���Ϊ������Ⱥ�ڶ������Ķ�������������ס�������Ʒ�Ƶĵ��������齨���������ң����˽⣬�ס�������Ʒ�Ƶĵ��Ե��۷ֱ�3100Ԫ��4600Ԫ��
��1��������ס�������Ʒ�Ƶĵ��Թ�50̨��ǡ��֧��200000Ԫ����ס�������Ʒ�Ƶĵ��Ը������˶���̨��
��2��������ס�������Ʒ�Ƶĵ��Թ�50̨��ÿ��Ʒ�����ٹ���һ̨����֧��������160000Ԫ�����м��ֹ�������˵�����ַ�����ʡǮ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��![]() Ϊֱ��
Ϊֱ��![]() ��һ�㣬
��һ�㣬![]() ƽ��
ƽ��![]() �������½�����ȷ����______����ֻ����ţ���
�������½�����ȷ����______����ֻ����ţ���![]() ��
��![]() ��Ϊ��ǣ�����
��Ϊ��ǣ�����![]() ����
����![]() ����
����![]() ;��
;��![]() ƽ��
ƽ��![]() ��
��

�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com