
分析 先判断$\sqrt{3}$在那两个整数之间,用小于$\sqrt{3}$的整数与10相加,得出整数部分,再用10+$\sqrt{3}$减去整数部分即可求出小数部分.
解答 解:∵$1<\sqrt{3}<2$,
∴$\sqrt{3}$的整数部分是1,
∴10+$\sqrt{3}$的整数部分是10+1=11,即x=11,
∴10+$\sqrt{3}$的小数部分是10+$\sqrt{3}$-11=$\sqrt{3}$-1,即y=$\sqrt{3}$-1,
∴x-y=11-($\sqrt{3}$-1)=11-$\sqrt{3}$+1=12-$\sqrt{3}$,
∴x-y的相反数为-(12-$\sqrt{3}$)=$\sqrt{3}$-12.
点评 本题考查了估算无理数的大小,解决本题的关键是估算出$\sqrt{3}$在1~2之间.


 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
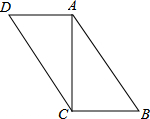 如图所示,在四边形ABCD中,已知AC⊥AD,AC=8,AD=x-10,CD=x-6,AB=10,BC=22-x.求证:四边形ABCD是平行四边形.
如图所示,在四边形ABCD中,已知AC⊥AD,AC=8,AD=x-10,CD=x-6,AB=10,BC=22-x.求证:四边形ABCD是平行四边形.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
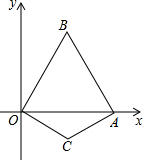 已知:如图,在直角坐标系xOy中,边长为2的等边△OAB的顶点B在第一象限,顶点A在x轴的正半轴上.另一等腰△OCA的顶点C在第四象限,OC=AC,∠C=120°.在等边△OAB的边上(点A除外)存在点D,使得△OCD为等腰三角形,请写出所有符合条件的点D的坐标($\frac{\sqrt{3}}{3}$,1),($\frac{2\sqrt{3}}{3}$0),($\frac{2}{3}$,0),($\frac{4}{3}$,$\frac{2\sqrt{3}}{3}$).
已知:如图,在直角坐标系xOy中,边长为2的等边△OAB的顶点B在第一象限,顶点A在x轴的正半轴上.另一等腰△OCA的顶点C在第四象限,OC=AC,∠C=120°.在等边△OAB的边上(点A除外)存在点D,使得△OCD为等腰三角形,请写出所有符合条件的点D的坐标($\frac{\sqrt{3}}{3}$,1),($\frac{2\sqrt{3}}{3}$0),($\frac{2}{3}$,0),($\frac{4}{3}$,$\frac{2\sqrt{3}}{3}$).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com