
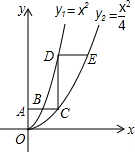
 如图,平行于x轴的直线AC分别交抛物线y1=x2(x≥0)与y2=$\frac{{x}^{2}}{4}$(x≥0)于B,C两点,过点C作y轴的平行交y1于点D,直线DE∥AC,交y2于点E,则$\frac{DE}{AB}$=2.
如图,平行于x轴的直线AC分别交抛物线y1=x2(x≥0)与y2=$\frac{{x}^{2}}{4}$(x≥0)于B,C两点,过点C作y轴的平行交y1于点D,直线DE∥AC,交y2于点E,则$\frac{DE}{AB}$=2. 分析 设A点坐标为(0,a),利用两个函数解析式求出点B、C的坐标,然后求出AB的长度,再根据CD∥y轴,利用y1的解析式求出D点的坐标,然后利用y2求出点E的坐标,从而得到DE的长度,然后求出比值即可得解.
解答 解:设A点坐标为(0,a),(a>0),
则x2=a,解得x=$\sqrt{a}$,
∴点B($\sqrt{a}$,a),
$\frac{{x}^{2}}{4}$=a,
则x=2$\sqrt{a}$,
∴点C(2$\sqrt{a}$,a), ∵CD∥y轴,
∵CD∥y轴,
∴点D的横坐标与点C的横坐标相同,为2$\sqrt{a}$,
∴y1=(2$\sqrt{a}$)2=4a,
∴点D的坐标为(2$\sqrt{a}$,4a),
∵DE∥AC,
∴点E的纵坐标为4a,
∴$\frac{{x}^{2}}{4}$=4a,
∴x=4$\sqrt{a}$,
∴点E的坐标为(4$\sqrt{a}$,4a),
∴DE=4$\sqrt{a}$-2$\sqrt{a}$=2$\sqrt{a}$,
∴则$\frac{DE}{AB}$=$\frac{2\sqrt{a}}{\sqrt{a}}$=2.
故答案为2.
点评 本题考查了二次函数的性质,二次函数图象上点的坐标特征,根据平行于x轴的点的纵坐标相同,平行于y轴的点的横坐标相同,用点A的纵坐标表示出各点的坐标是解题的关键.


科目:初中数学 来源: 题型:选择题
| A. | 1:2:1:2 | B. | 1:2:2:1 | C. | 1:2:3:4 | D. | 1:1:2:2 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
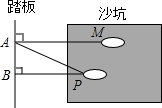 如图,是李晓松同学在运动会跳远比赛中最好的一跳,甲、乙、丙三名同学分别测得PA=5.52米,PB=5.37米,MA=5.60米,那么他的跳远成绩应该为5.37米.
如图,是李晓松同学在运动会跳远比赛中最好的一跳,甲、乙、丙三名同学分别测得PA=5.52米,PB=5.37米,MA=5.60米,那么他的跳远成绩应该为5.37米.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
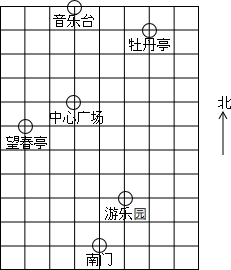 春天到了,七(1)班组织同学到人民公园春游,张明、李华对着景区示意图描述牡丹亭位置(图中小正方形边长代表100m)
春天到了,七(1)班组织同学到人民公园春游,张明、李华对着景区示意图描述牡丹亭位置(图中小正方形边长代表100m)查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com