
分析 由于a、b、c均为实数,且abc=1,可得到ac=$\frac{1}{b}$,然后把原式变形为$\frac{abc}{a+ab+abc}$+$\frac{1}{b+bc+1}$+$\frac{1}{c+\frac{1}{b}+1}$,再进行约分后进行分式的加法运算即可得到答案.
解答 解:∵a、b、c均为实数,且abc=1,则ac=$\frac{1}{b}$,
∴原式=$\frac{abc}{a+ab+abc}$+$\frac{1}{b+bc+1}$+$\frac{1}{c+\frac{1}{b}+1}$
=$\frac{bc}{b+bc+1}$+$\frac{1}{b+bc+1}$+$\frac{b}{b+bc+1}$
=$\frac{bc+b+1}{b+bc+1}$
=1.
点评 本题考查了分式的化简求值:先把各分子或分母因式分解,再进行乘除运算(除法运算转化为乘法运算),然后进行加减运算,最后把满足条件的字母的值代入进行计算求值.也考查了代数式的变形能力.


 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
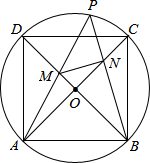 如图,正方形ABCD内接于⊙O,P为劣弧$\widehat{CD}$上一点,PA交BD于点M,PB交AC于点N,记∠PBD=θ.若MN⊥PB,则2cos2θ-tanθ的值( )
如图,正方形ABCD内接于⊙O,P为劣弧$\widehat{CD}$上一点,PA交BD于点M,PB交AC于点N,记∠PBD=θ.若MN⊥PB,则2cos2θ-tanθ的值( )| A. | $\frac{1}{2}$ | B. | 1 | C. | $\frac{{\sqrt{2}}}{2}$ | D. | $\frac{{\sqrt{2}}}{4}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
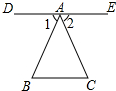 如图,有下列三个条件:①DE∥BC;②∠1=∠2;③∠B=∠C.
如图,有下列三个条件:①DE∥BC;②∠1=∠2;③∠B=∠C.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com