
 如图所示,在等腰Rt△ABC中,AD平分∠BAC,BD⊥AD,BC交AD于F.
如图所示,在等腰Rt△ABC中,AD平分∠BAC,BD⊥AD,BC交AD于F.| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
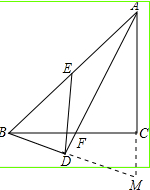 ∵BD⊥AD,
∵BD⊥AD,
|
| 1 |
| 2 |
|
| 1 |
| 2 |
| 1 |
| 2 |


 一课一练课时达标系列答案
一课一练课时达标系列答案科目:初中数学 来源: 题型:
 如图,程程和小磊在他们家附近的公园中玩跷跷板,跷跷板上的横板AD通过点B,且可以绕点B上下转动,木桩BC与路面AC始终成90°,当处在如图所示的位置时∠ABC=60°,则这个跷跷板上下最多可以转动( )
如图,程程和小磊在他们家附近的公园中玩跷跷板,跷跷板上的横板AD通过点B,且可以绕点B上下转动,木桩BC与路面AC始终成90°,当处在如图所示的位置时∠ABC=60°,则这个跷跷板上下最多可以转动( )| A、180° | B、120° |
| C、90° | D、60° |
查看答案和解析>>
科目:初中数学 来源: 题型:
 为了了解某校500名七年级新生入学时的数学水平,随机抽取若干名学生的数学成绩统计整理后绘制如图的频数分布直方图,观察图形回答下列问题:
为了了解某校500名七年级新生入学时的数学水平,随机抽取若干名学生的数学成绩统计整理后绘制如图的频数分布直方图,观察图形回答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,已知:点E在△ABC的边AB上,∠C=90°,以AE为直径的⊙O切BC于D.
如图,已知:点E在△ABC的边AB上,∠C=90°,以AE为直径的⊙O切BC于D.| 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com