
 如图,在平面直角坐标系中,有一组有规律的点:A1(0,1)、A2(1,0)、A3(2,1)、A4(3,0)、A5(4,1),…依此规律可知,当n为奇数时,有点An(n-1,1);当n为偶数时,有点An(n-1,0).抛物线C1经过A1、A2、A3三点,抛物线C2经过A2、A3、A4三点,抛物线C3经过抛物线A3、A4、A5三点,…,抛物线Cn经过An、An+1、An+2.
如图,在平面直角坐标系中,有一组有规律的点:A1(0,1)、A2(1,0)、A3(2,1)、A4(3,0)、A5(4,1),…依此规律可知,当n为奇数时,有点An(n-1,1);当n为偶数时,有点An(n-1,0).抛物线C1经过A1、A2、A3三点,抛物线C2经过A2、A3、A4三点,抛物线C3经过抛物线A3、A4、A5三点,…,抛物线Cn经过An、An+1、An+2.分析 (1)根据顶点式即可求出C1,C4的解析式;
(2)由特殊出发,可以发现抛物线C27、C28的解析式应该为:y27=(x-27)2,y28=-(x-28)2+1.则得到点E(30,9)、F(30,5),根据两点之间的距离公式即可求得EF;
(3)分两种情况:在A1000(999,0)点左侧;在A1000(999,0)点右侧;根据三角函数即可得到sin∠PA1000N的值.
解答 解:(1)∵A1(0,1)、A2(1,0)、A3(2,1)
∴A1(0,1)、A3(2,1)关于x=1对称,
∴C1的对称轴为x=1,
同理C2的对称轴为x=2,
故答案为1,2;
由顶点式求出C3的解析式为:y=(x-3)2,C4的解析式为:y=-(x-4)2+1.
(2)由特殊出发,可以发现这组抛物线解析式的特点:
y1=(x-1)2,
y2=-(x-2)2+1,
y3=(x-3)2,
y4=-(x-4)2+1,
…
∴抛物线C27、C28的解析式应该为:y27=(x-27)2,y28=-(x-28)2+1.
∴当e=30时,f1=(30-27)2=9,f2=(30-28)2+1=5,
∴EF=f1-f2=4.
(3)由(2)中发现的规律可知,抛物线C999、C1000解析式分别为:y=(x-999)2,
y=-(x-1000)2+1.
点A1000坐标为(999,0).
顺便指向,由(2)的研究经验发现,可以退回简单的抛物线C3、C4的情况来研究.分以下两种情况,如图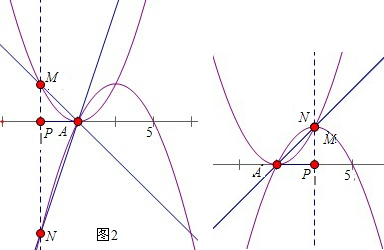
在A1000(999,0)点左侧,当m=998时,M(998,1)此时有∠PA1000M=45°,N(998,-3),相应的sin∠PA1000N的值为$\frac{3\sqrt{10}}{10}$;
在A1000(999,0)点右侧,当m=1000时,M(1000,1)此时有∠PA1000M=45°,N(1000,1),相应的sin∠PA1000N的值为$\frac{\sqrt{2}}{2}$.
点评 考查了二次函数综合题,涉及的知识点有:顶点式求抛物线的解析式,两点之间的距离公式,勾股定理逆定理,分类思想的应用,三角函数的知识.综合性较强,有一定的难度.


 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
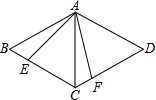 如图,AC是菱形ABCD的对角线,∠B=60°,以点A为顶点作∠EAF=60°,∠EAF的两边分别交BC,CD于点E,F.
如图,AC是菱形ABCD的对角线,∠B=60°,以点A为顶点作∠EAF=60°,∠EAF的两边分别交BC,CD于点E,F.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
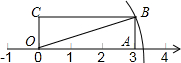 如图所示,矩形OABC的边长OA长为3,边AB长为1,OA在数轴上,以O为圆心,OB为半径画弧,交正半轴于一点,则这个点表示的实数是( )
如图所示,矩形OABC的边长OA长为3,边AB长为1,OA在数轴上,以O为圆心,OB为半径画弧,交正半轴于一点,则这个点表示的实数是( )| A. | 4 | B. | 2$\sqrt{2}$ | C. | $\sqrt{10}$ | D. | 3.5 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com