
如图,以扇形OAB的顶点O为原点,半径OB所在的直线为x轴,建立平面直角坐标系,点B的坐标为(2,0),若抛物线y= x2+k与扇形OAB的边界总有两个公共点,则实数k的取值范围是 .
x2+k与扇形OAB的边界总有两个公共点,则实数k的取值范围是 .

﹣2<k<
【解析】
试题分析:根据∠AOB=45°求出直线OA的解析式,然后与抛物线解析式联立求出有一个公共点时的k值,即为一个交点时的最大值,再求出抛物线经过点B时的k的值,即为一个交点时的最小值,然后写出k的取值范围即可.
由图可知,∠AOB=45°,
∴直线OA的解析式为y=x,
联立 消掉y得,
消掉y得,
x2﹣2x+2k=0,
△=(﹣2)2﹣4×1×2k=0,
即k= 时,抛物线与OA有一个交点,
时,抛物线与OA有一个交点,
此交点的横坐标为1,
∵点B的坐标为(2,0),
∴OA=2,
∴点A的坐标为( ,
, ),
),
∴交点在线段AO上;
当抛物线经过点B(2,0)时, ×4+k=0,
×4+k=0,
解得k=﹣2,
∴要使抛物线y= x2+k与扇形OAB的边界总有两个公共点,实数k的取值范围是﹣2<k<
x2+k与扇形OAB的边界总有两个公共点,实数k的取值范围是﹣2<k< .
.
故答案为:﹣2<k<
 .
.
考点: 二次函数的性质.


科目:初中数学 来源: 题型:
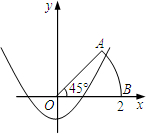 (2013•兰州)如图,以扇形OAB的顶点O为原点,半径OB所在的直线为x轴,建立平面直角坐标系,点B的坐标为(2,0),若抛物线y=
(2013•兰州)如图,以扇形OAB的顶点O为原点,半径OB所在的直线为x轴,建立平面直角坐标系,点B的坐标为(2,0),若抛物线y=| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,以扇形OAB的顶点O为原点,半径OB所在的直线为x轴,建立平面直角坐标系,点B的坐标为(2,0),若抛物线y=x2+k与扇形OAB的边界总有两个公共点,则实数k的取值范围是
如图,以扇形OAB的顶点O为原点,半径OB所在的直线为x轴,建立平面直角坐标系,点B的坐标为(2,0),若抛物线y=x2+k与扇形OAB的边界总有两个公共点,则实数k的取值范围是| 1 |
| 2 |
| 1 |
| 2 |
查看答案和解析>>
科目:初中数学 来源:2013-2014学年江西省九年级3月月考数学试卷(解析版) 题型:填空题
如图,以扇形OAB的顶点O为原点,半径OB所在的直线为 轴,建立平面直角坐标系,点B的坐标为(2,0),若抛物线
轴,建立平面直角坐标系,点B的坐标为(2,0),若抛物线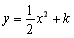 与扇形OAB的边界总有两个公共点,则实数
与扇形OAB的边界总有两个公共点,则实数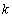 的取值范围是?????????????????? .
的取值范围是?????????????????? .

查看答案和解析>>
科目:初中数学 来源:2013年甘肃省兰州市中考数学试卷(解析版) 题型:填空题
 x2+k与扇形OAB的边界总有两个公共点,则实数k的取值范围是 .
x2+k与扇形OAB的边界总有两个公共点,则实数k的取值范围是 .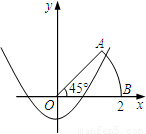
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com