
【题目】如图⊙O是ABC的外接圆,且AB=AC,点D在弧BC上运动,过点D作DE//BC,DE交AB的延长线于点E,连结AD、BD

(1)求证∠ADB=∠E;
(2)当点D运动到什么位置时,DE是⊙O的切线?请说明理由;
(3)当AB=5,BC=6时,求⊙O的半径.
【答案】(1)证明见解析;(2)当点D是弧BC的中点时,DE是⊙O的切线,理由见解析;(3) ![]() .
.
【解析】
试题(1)运用圆周角定理,以及平行线的性质得出角之间的关系,得出相等关系;
(2)当点D运动到弧BC中点时,DE是⊙O的切线,理由为:由D为弧BC中点,利用垂径定理的逆定理得到AD垂直于BC,且AD过圆心,由BC与DE平行,利用与平行线中的一条垂直,与另一条也垂直得到AD与DE垂直,即可确定出DE为圆的切线.
(3)连接BO,AO,延长AO交BC于点F,由等腰三角形的性质得到AF与BC垂直,且F为BC的中点,求出BF的长,在直角三角形ABF中,理由勾股定理求出AF的长,设圆O的半径为r,在直角三角形OBF中,由AF-AO表示出OF,利用勾股定理列出关于r的方程,求出方程的解即可得到圆的半径长.
试题解析: (1)证明:在ABC中,∵AB=AC,∴∠ABC=∠C
∵DE//BC,∴∠ABC=∠E,∴∠E=∠C
∵∠ADB=∠C
∴∠ADB=∠E
(2)当点D是弧BC的中点时,DE是⊙O的切线
理由:当点D是弧BC的中点时,则有AD⊥BC,且AD过圆心O,如图:

∵DE//BC,∴AD⊥ED
∴DE是⊙O的切线
(3)∵AB=5,∴AF=4
设⊙O的半径为r,在RtOBF中,DF=4-r,OB=r,BF=3.
∴r2=32+(4-r)2,解得r=![]()
∴⊙O的半径是![]() .
.
考点: 1.圆周角定理;2.平行线的性质;3.等腰三角形的性质.


 全能练考卷系列答案
全能练考卷系列答案科目:初中数学 来源: 题型:
【题目】如图,![]() 在平面直角坐标系中,
在平面直角坐标系中,![]() ,
,![]() ,
,![]() ,点
,点![]() 、
、![]() 在
在![]() 轴上且关于
轴上且关于![]() 轴对称.
轴对称.
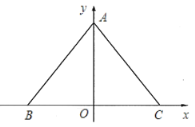
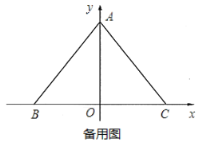

(1)求点![]() 的坐标;
的坐标;
(2)动点![]() 以每秒2个单位长度的速度从点
以每秒2个单位长度的速度从点![]() 出发沿
出发沿![]() 轴正方向向终点
轴正方向向终点![]() 运动,设运动时间为
运动,设运动时间为![]() 秒,点
秒,点![]() 到直线
到直线![]() 的距离
的距离![]() 的长为
的长为![]() ,求
,求![]() 与
与![]() 的关系式;
的关系式;
(3)在(2)的条件下,当点![]() 到
到![]() 的距离
的距离![]() 为
为![]() 时,连接
时,连接![]() ,作
,作![]() 的平分线分别交
的平分线分别交![]() 、
、![]() 于点
于点![]() 、
、![]() ,求
,求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠B=90°,AB=12,BC=24,动点P从点A开始沿边AB向终点B以每秒2个单位长度的速度移动,动点Q从点B开始沿边BC以每秒4个单位长度的速度向终点C移动,如果点P、Q分别从点A、B同时出发,那么△PBQ的面积S随出发时间t(s)如何变化?写出函数关系式及t的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
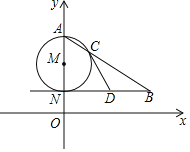
【题目】如图,AN是⊙M的直径,NB∥x轴,AB交⊙M于点C.
(1)若点A(0,6),N(0,2),∠ABN=30°,求点B的坐标;
(2)若D为线段NB的中点,求证:直线CD是⊙M的切线.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了解初中生的交通安全知识掌握情况,在本校初中部随机抽取10﹪的学生,进行了交通安全知识测试,得分情况如下两个统计图,并约定85分及以上为优秀;73分~84分为良好;60分~72分为合格;59分及以下为不合格(满分为100分).
【1】在抽取的学生中,不合格人数所占的百分比是 ;
【2】若不合格学生的总分恰好等于其他等级的某一个学生的分数,请推测这个学生是什么等级?并估算出该校初中部学生中共有多少人不合格?
【3】试求所抽取的学生的平均分.
 .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,C是![]() 的中点,CE⊥AB于 E,BD交CE于点F.
的中点,CE⊥AB于 E,BD交CE于点F.
(1)若CD ﹦6, AC ﹦8,求⊙O的半径
(2)求证:CF﹦BF;

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为厉行节能减排,倡导绿色出行,今年3月以来.“共享单车”(俗称“小黄车”)公益活动登陆我市中心城区,某公司拟在甲、乙两个街道社区投放一批“小黄车”,这批自行车包括A、B两种不同款型,请回答下列问题:
问题1:单价
该公司早期在甲街区进行了试点投放,共投放A、B两型自行车各50辆,投放成本共计7500元,其中B型车的成本单价比A型车高10元,A、B两型自行车的单价各是多少?
问题2:投放方式
该公司决定采取如下投放方式:甲街区每1000人投放a辆“小黄车”,乙街区每1000人投放![]() 辆“小黄车”,按照这种投放方式,甲街区共投放1500辆,乙街区共投放1200辆,如果两个街区共有15万人,试求a的值.
辆“小黄车”,按照这种投放方式,甲街区共投放1500辆,乙街区共投放1200辆,如果两个街区共有15万人,试求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,抛物线y=ax2+bx经过点A(2,4)和点B(6,0).
(1)求这条抛物线所对应的二次函数的解析式;
(2)直接写出它的开口方向、顶点坐标;
(3)点(x1,y1),(x2,y2)均在此抛物线上,若x1>x2>4,则y1 ________ y2(填“>”“=”或“<”).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一列快车由甲地开往乙地,一列慢车由乙地开往甲地,两车同时出发,匀速运动,快车离乙地的路程![]() (
(![]() )与行驶的时间
)与行驶的时间![]() (
(![]() )之间的函数关系,如图中线段
)之间的函数关系,如图中线段![]() 所示,慢车离乙地的路程
所示,慢车离乙地的路程![]() (
(![]() )与行驶的时间
)与行驶的时间![]() (
(![]() )之间的函数关系,如图中线段
)之间的函数关系,如图中线段![]() 所示,则快、慢车相距225
所示,则快、慢车相距225![]() 时,行驶的时间是( )
时,行驶的时间是( )

A.1![]() B.3
B.3![]() C.1
C.1![]() 或3
或3![]() D.2
D.2![]() 或4
或4![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com