
分析 (1)①首先根据a=1求得A的坐标,然后代入二次函数的解析式,求得m的值即可确定二次函数的解析式;
②根据解析式确定抛物线与坐标轴的交点坐标,从而确定三角形的面积;
(2)将原二次函数配方后即可确定其对称轴为x=m,然后根据A、B两点关于x=m对称得到a+n-m=m-a,从而确定a、m、n之间的关系;
(3)根据a=m-$\frac{3}{2}$得到A(m-$\frac{3}{2}$,0)代入y=(x-m)2-m2+3得0=(m-$\frac{3}{2}$-m)2-m2+3,求得m的值即可确定a的值.
解答 解:(1)①∵a=1,
∴A(1,0),
代入y=x2-2mx+3得1-2m+3=0,解得m=2,
∴y=x2-4x+3;
②在y=x2-4x+3中,当y=0时,有x2-4x+3=0可得x=1或x=3,
∴A(1,0)、B(3,0),
∴AB=2再根据解析式求出C点坐标为(0,3),
∴OC=3,
△ABC的面积=$\frac{1}{2}$×2×3=3;
(2)∵y=x2-2mx+3=(x-m)2-m2+3,
∴对称轴为直线x=m,
∵二次函数y=x2-2mx+3的图象与x轴交于点A和点B
∴点A和点B关于直线x=m对称,
∴a+n-m=m-a,
∴a=m-$\frac{n}{2}$;
(3)y=x2-2mx+3(m>$\sqrt{3}$)化为顶点式为y=(x-m)2-m2+3(m>$\sqrt{3}$)
①当a为整数,因为n>0且n为整数 所以a+n是整数,
∵线段AB(包括A、B)上有且只有三个点的横坐标是整数,
∴n=2,
∴a=m-1,
∴A(m-1,0)代入y=(x-m)2-m2+3得(x-m)2-m2+3=0,
∴m2-4=0,
∴m=2,m=-2(舍去),
∴a=2-1=1,
②当a不是整数,因为n>0且n为整数 所以a+n不是整数,
∵线段AB(包括A、B)上有且只有三个点的横坐标是整数,
∴n=3,
∴a=m-$\frac{3}{2}$,
∴A(m-$\frac{3}{2}$,0)代入y=(x-m)2-m2+3得0=(m-$\frac{3}{2}$-m)2-m2+3,
∴m2=$\frac{21}{4}$,
∴m=$\frac{\sqrt{21}}{2}$,m=-$\frac{\sqrt{21}}{2}$(舍去),
∴a=$\frac{\sqrt{21}}{2}-\frac{3}{2}$,
综上所述:a=1或a=$\frac{\sqrt{21}}{2}-\frac{3}{2}$.
点评 本题考查了二次函数的综合知识,其中涉及到的知识点有抛物线的顶点公式和三角形的面积求法.在求有关动点问题时要注意分析题意分情况讨论结果.


科目:初中数学 来源: 题型:解答题
 如图,平面直角坐标系中,A、C两点的坐标分别是A(0,4),C(8,0),以OA、OC为邻边作矩形OABC,然后以AC为折痕折叠矩形,使B点落在第四象限的E处,AE交x轴于D点,连接CE并延长交y轴于F点.
如图,平面直角坐标系中,A、C两点的坐标分别是A(0,4),C(8,0),以OA、OC为邻边作矩形OABC,然后以AC为折痕折叠矩形,使B点落在第四象限的E处,AE交x轴于D点,连接CE并延长交y轴于F点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
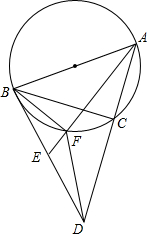 如图,已知在△ABC中,AB>BC,过点B作△ABC的外接圆的切线,交AC的延长线于点D,E为BD的中点,连接AE交△ABC的外接圆于点F,求证:∠CBF=∠BDF.
如图,已知在△ABC中,AB>BC,过点B作△ABC的外接圆的切线,交AC的延长线于点D,E为BD的中点,连接AE交△ABC的外接圆于点F,求证:∠CBF=∠BDF.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,抛物线y=-$\frac{1}{2}$x2+2与x轴交于A、B两点,其中点A在x轴的正半轴上,点B在x轴的负半轴上
如图,抛物线y=-$\frac{1}{2}$x2+2与x轴交于A、B两点,其中点A在x轴的正半轴上,点B在x轴的负半轴上查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,正方形ABCD的边长为2,点E,F分别是DC和BC两边上的动点且始终保持∠EAF=45°,连接AE与AF交DB于点N,M.下列结论:①△ADM∽△NBA;②△CEF的周长始终保持不变其值是4;③AE×AM=AF×AN;④DN2+BM2=NM2.其中正确的结论是( )
如图,正方形ABCD的边长为2,点E,F分别是DC和BC两边上的动点且始终保持∠EAF=45°,连接AE与AF交DB于点N,M.下列结论:①△ADM∽△NBA;②△CEF的周长始终保持不变其值是4;③AE×AM=AF×AN;④DN2+BM2=NM2.其中正确的结论是( )| A. | ①②③ | B. | ①②④ | C. | ②③④ | D. | ①③④ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知在四边形ABCD中,AB=CD,BC=AD,E、F分别是对角线AC上两点,且AE=CF.
已知在四边形ABCD中,AB=CD,BC=AD,E、F分别是对角线AC上两点,且AE=CF.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com