
”¾ĢāÄæ”æČēĶ¼1£¬ŌŚ”÷ABCÖŠ£¬”ĻBAC=90”ć£¬AB=AC£¬BDĘ½·Ö”ĻABC£®
£Ø1£©ŃÓ³¤BAµ½M£¬Ź¹AM=AD£¬Į¬½ÓCM£¬Ēó”ĻACMµÄ¶ČŹż£®
£Ø2£©ČēĶ¼2£¬ČōCE”ĶBDÓŚE£¬ŌņBDÓėEC“ęŌŚŌõŃłµÄŹżĮæ¹ŲĻµ£æĒėĖµĆ÷ĄķÓÉ.
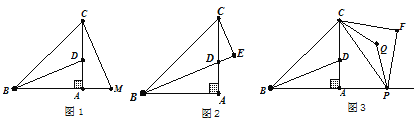
£Ø3£©ČēĶ¼3£¬µćPŹĒÉäĻßBAÉĻAµćÓŅ±ßŅ»¶Æµć£¬ŅŌCPĪŖŠ±±ß×÷µČŃüÖ±½Ē”÷CPF£¬ĘäÖŠ”ĻF=90”ć£¬µćQĪŖ”ĻFCPÓė”ĻCPFµÄ½ĒĘ½·ÖĻߵĽ»µć£®µ±µćPŌĖ¶ÆŹ±£¬µćQŹĒ·ńŅ»¶ØŌŚÉäĻßBDÉĻ£æČōŌŚ£¬ĒėÖ¤Ć÷£»Čō²»ŌŚ£¬ĒėĖµĆ÷ĄķÓÉ£®
”¾“š°ø”æ£Ø1£©22.5”ć£»£Ø2£©BD=2CE£¬ĄķÓɼū½āĪö£»£Ø3£©µćQŅ»¶ØŌŚÉäĻßBDÉĻ.
”¾½āĪö”æŹŌĢā·ÖĪö: £Ø1£©ĶعżÖ¤Ć÷”÷BDA”Õ”÷MCA,µĆµ½”ĻDBA=”ĻMCA,ŌŁøł¾ŻBDĘ½·Ö”ĻABCµĆ”ĻABD£½22.5”ć£¬µĆµ½”ĻACM£½22.5”ć£»
(2)ŃÓ³¤CE½»BAµÄŃÓ³¤ĻßÓŚµćG£¬ĶعżÅŠ¶Ø”÷ABD”Õ”÷ACG£¬µĆ³öBD£½CG£½2CE¼“æÉ£»
(3)Į¬½ÓCQ£¬¹żµćQ×÷QM”ĶBPÓŚM£¬×÷QN”ĶBCÓŚN£¬ŌŚµČŃüÖ±½Ē”÷CPFÖŠ£¬ĒóµĆ”ĻQCP£½”ĻQPC£½22.5”ć£¬½ų¶ųµĆ³ö”÷PQCÖŠ£¬”ĻPQC£½135”ć£»ŌŚĖıߊĪQNBMÖŠ£¬øł¾ŻQM”ĶBP£¬QN”ĶBC£¬”ĻABC£½45”ć£¬µĆµ½”ĻMQN£½135”ć£¬½ų¶ųµĆµ½”ĻNQC£½”ĻMQP£¬øł¾ŻAASÅŠ¶Ø”÷QPM”Õ”÷QCN£¬µĆ³öQM£½QN£¬×īŗóøł¾Ż½ĒĘ½·ÖĻߵĊŌÖŹ¶ØĄķµÄÄę¶ØĄķ£¬µĆ³öµćQŅ»¶ØŌŚÉäĻßBDÉĻ£®
ŹŌĢā½āĪö:
£Ø1£©”ß”ĻBAC£½90”ć£¬
”ą”ĻCAM=90”ć,
”ą”ĻBAC£½”ĻCAM£¬
ÓÖ”ßAB£½AC£¬AM=AD£¬
”ą”÷BDA”Õ”÷MCA,
”ą”ĻDBA=”ĻMCA,
”ßBDĘ½·Ö”ĻABC,
”ą”ĻABD£½22.5”ć£¬
”ą”ĻACM £½22.5”ć£»
¹Ź“š°øĪŖ£ŗ22.5”ć£®
£Ø2£©ČēĶ¼£¬ŃÓ³¤CE½»BAµÄŃÓ³¤ĻßÓŚµćG£¬
”ßBDĘ½·Ö”ĻABC£¬CE”ĶBD£¬
”ąCE£½GE£¬
ŌŚ”÷ABDÓė”÷ACGÖŠ£¬
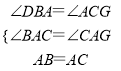 £¬
£¬
”ą”÷ABD”Õ”÷ACG£ØAAS£©£¬
”ąBD£½CG£½2CE£»
£Ø3£©µćQŅ»¶ØŌŚÉäĻßBDÉĻ£¬
ĄķÓÉ£ŗČēĶ¼£¬Į¬½ÓCQ£¬¹żµćQ×÷QM”ĶBPÓŚM£¬×÷QN”ĶBCÓŚN£¬
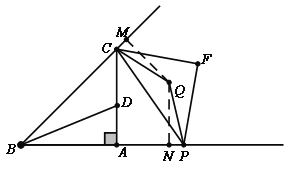
”ßQFĪŖ”ĻPFCµÄ½ĒĘ½·ÖĻߣ¬”÷CPFĪŖµČŃüÖ±½ĒČż½ĒŠĪ£¬
”ąQFĪŖPCµÄ“¹Ö±Ę½·ÖĻߣ¬
”ąPQ£½QC£¬
”ßQĪŖ”ĻFPCÓė”ĻPFCµÄ½ĒĘ½·ÖĻߵĽ»µć£¬
”ąCQĘ½·Ö”ĻFCP£¬
”ß”÷CPFĪŖµČŃüÖ±½ĒČż½ĒŠĪ£¬
”ą”ĻFCP£½”ĻFPC£½45”ć£¬
”ą”ĻQCP£½”ĻQPC£½22.5”ć£¬
”ą”÷PQCÖŠ£¬”ĻPQC£½135”ć£¬
”ßŌŚĖıߊĪQNBMÖŠ£¬QM”ĶBP£¬QN”ĶBC£¬”ĻABC£½45”ć£¬
”ą”ĻMQN£½135”ć£¬
”ą”ĻMQN£½”ĻPQC£¬
”ą”ĻNQC£½”ĻMQP£¬
ÓÖ”ßQC£½QP£¬QM”ĶBP£¬QN”ĶBC£¬
”ą”÷QPM”Õ”÷QCN£ØAAS£©£¬
”ąQM£½QN£¬
ÓÖ”ßQM”ĶBP£¬QN”ĶBC£¬
”ąµćQŅ»¶ØŌŚÉäĻßBDÉĻ£®
µć¾¦: ±¾ĢāÖ÷ŅŖæ¼²éĮĖČż½ĒŠĪµÄ×ŪŗĻÓ¦ÓĆ£¬½āĢāŹ±ŠčŅŖŌĖÓĆČż½ĒŠĪÄŚ½ĒŗĶ¶ØĄķ”¢µČŃüÖ±½ĒČż½ĒŠĪµÄŠŌÖŹ”¢½ĒĘ½·ÖĻߵĶØŅåŅŌ¼°Č«µČČż½ĒŠĪµÄÅŠ¶ØÓėŠŌÖŹµČÖŖŹ¶£®½ā¾öĪŹĢāµÄ¹Ų¼üŹĒ×÷øØÖśĻߣ¬¹¹ŌģČ«µČČż½ĒŠĪ£¬øł¾ŻČ«µČČż½ĒŠĪµÄŠŌÖŹ½ųŠŠĶʵ¼£®½āĢāŹ±×¢Ņā£ŗµ½½ĒĮ½±ß¾ąĄėĻąµČµÄµćŌŚÕāøö½ĒµÄĘ½·ÖĻßÉĻ£®



| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æ2020Äź1ŌĀ13ČÕ£¬ÖŠ¹śĘū³µ¹¤ŅµŠ»į¹«²¼µÄŹż¾ŻĻŌŹ¾£ŗ2019Äź£¬ÖŠ¹śĘū³µĄŪ¼ĘÉś²śŌ¼25 700000Į¾£®Źż¾Ż25700000ÓĆæĘѧ¼ĒŹż·Ø±ķŹ¾ĪŖ£Ø £©
A.257”Į105B.25.7”Į106C.2.57”Į107D.0.257”Į108
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æÅ×ĪļĻßy=£Øx©2£©2+3µÄ¶Ō³ĘÖįŹĒ£Ø £©
A.Ö±Ļßx=2
B.Ö±Ļßx=3
C.Ö±Ļßx=©2
D.Ö±Ļßx=©3
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŌŚĘ½ĆęÖ±½Ē×ų±źĻµxoyÖŠ£¬µćA”¢B”¢CµÄ×ų±ź·Ö±šĪŖ£Ø-1£¬0£©”¢£Ø-2£¬3£©”¢£Ø-3£¬1£©£®
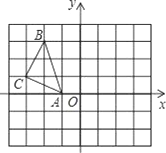
£Ø1£©×÷³ö”÷ABC¹ŲÓŚxÖį¶Ō³ĘµÄ ”÷A1B1C1£¬²¢Š“³öB1”¢C1
Į½µćµÄ×ų±ź£ŗB1: £¬ C1: £®
£Ø2£©”÷ABCµÄĆ껿S”÷ABC= £®
£Ø3£©ČōDµćŌŚyÖįÉĻŌĖ¶Æ£¬ĒóCD+DAµÄ×īŠ”Öµ£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æĻĀĮŠ¼ĘĖćÕżČ·µÄŹĒ£Ø £©
A.7a©4a=3B.£Ø2a2£©3=8a6
C.3a£Ø©2a£©3=24a4D.a3+2a=2a4
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æĖę×ÅŅĘ¶Æ»„ĮŖĶųµÄæģĖŁ·¢Õ¹£¬¹²Ļķµ„³µŌŚÓąŅ¦µÄ“ó½ÖŠ”ĻļĖę“¦æ“¼ū£¬½ā¾öĮĖŗܶąČĖµÄ½»ĶسöŠŠĪŹĢā£¬ĄīĄĻŹ¦ŌēÉĻĘļµ„³µÉĻ°ą£¬ÖŠĶ¾ŅņµĄĀ·Ź©¹¤ĶĘ³µ²½ŠŠĮĖŅ»¶ĪĀ·£¬µ½Ń§Š£¹²ÓĆŹ±15·ÖÖÓ£¬Čē¹ūĖūĘļµ„³µµÄĘ½¾łĖŁ¶ČŹĒĆæ·ÖÖÓ250Ć×£¬ĶĘ³µ²½ŠŠµÄĘ½¾łĖŁ¶ČŹĒĆæ·ÖÖÓ80Ć×£¬Ėū¼ŅĄėѧŠ£µÄĀ·³ĢŹĒ2900Ć×£¬ĒóĖūĶĘ³µ²½ŠŠĮĖ¶ąÉŁ·ÖÖÓ£æ
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
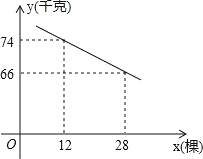
”¾ĢāÄæ”æÄ³Ę¬¹ūŌ°ÓŠ¹ūŹ÷80æĆ£¬ĻÖ×¼±ø¶ąÖÖŅ»Š©¹ūŹ÷Ģįøß¹ūŌ°²śĮ棬µ«ŹĒČē¹ū¶ąÖÖŹ÷£¬ÄĒĆ“Ź÷Ö®¼äµÄ¾ąĄėŗĶĆææĆŹ÷ĖłŹÜ¹āÕÕ¾Ķ»į¼õÉŁ£¬µ„æĆŹ÷µÄ²śĮæĖęÖ®½µµĶ£®ČōøĆ¹ūŌ°ĆææĆ¹ūŹ÷²ś¹ūy£ØĒ§æĖ£©£¬ŌöÖÖ¹ūŹ÷x£ØæĆ£©£¬ĖüĆĒÖ®¼äµÄŗÆŹż¹ŲĻµČēĶ¼ĖłŹ¾£®
£Ø1£©ĒóyÓėxÖ®¼äµÄŗÆŹż¹ŲĻµŹ½£»
£Ø2£©ŌŚĶ¶Čė³É±¾×īµĶµÄĒéæöĻĀ£¬ŌöÖÖ¹ūŹ÷¶ąÉŁæĆŹ±£¬¹ūŌ°æÉŅŌŹÕ»ń¹ūŹµ6750Ē§æĖ£æ
£Ø3£©µ±ŌöÖÖ¹ūŹ÷¶ąÉŁæĆŹ±£¬¹ūŌ°µÄ×ܲśĮæw£ØĒ§æĖ£©×ī“ó£æ×ī“ó²śĮæŹĒ¶ąÉŁ£æ
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æÖ±ĻßAB”ĪCD£¬EĪŖÖ±ĻßAB”¢CDÖ®¼äµÄŅ»µć£®
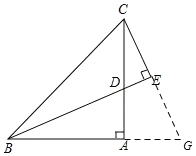
£Ø1£©ČēĶ¼1£¬Čō”ĻB=15”ć£¬”ĻBED=90”ć£¬Ōņ”ĻD=”ć£»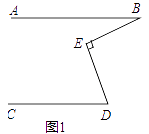
£Ø2£©ČēĶ¼2£¬Čō”ĻB=¦Į£¬”ĻD=¦Ā£¬Ōņ”ĻBED=£»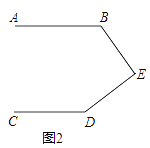
£Ø3£©ČēĶ¼3£¬Čō”ĻB=¦Į£¬”ĻC=¦Ā£¬Ōņ¦Į”¢¦ĀÓė”ĻBECÖ®¼äÓŠŹ²Ć“µČĮæ¹ŲĻµ£æĒė²ĀĻėÖ¤Ć÷£®
²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com