
分析 (1)首先根据题意可知总工作量为30×8=240吨不变,故卸货速度v与卸货时间t之间为反比例关系,即vt=240,变形即可得出v关于t的函数关系式;
(2)由v=$\frac{240}{t}$得出t=$\frac{240}{v}$,再将t≤5代入,即可求出v的取值范围.
解答 解:(1)设轮船上的货物总量为k吨,根据已知条件得k=30×8=240,
所以v关于t的函数关系式为v=$\frac{240}{t}$;
(2)∵v=$\frac{240}{t}$,
∴t=$\frac{240}{v}$,
∵t≤5,
∴$\frac{240}{v}$≤5,
解得v≥48.
即平均每天至少要卸载48吨.
点评 本题考查反比例函数的应用,解答该类问题的关键是确定两个变量之间的函数关系,然后利用待定系数法求出它们的关系式,进一步根据题意求解.


 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
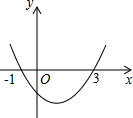 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,它与x轴的两个交点分别为(-1,0)和(3,0).对于下列结论:①abc>0;②b-2a=0;③a-b+c<0;④a+b+c>0;⑤b2-4ac>0.其中结论正确的是( )
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,它与x轴的两个交点分别为(-1,0)和(3,0).对于下列结论:①abc>0;②b-2a=0;③a-b+c<0;④a+b+c>0;⑤b2-4ac>0.其中结论正确的是( )| A. | ①②⑤ | B. | ①⑤ | C. | ②③ | D. | ①②③④⑤ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
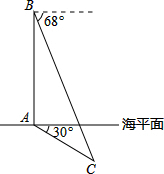 我海军在我国的南海海域举行反潜实战演习.在演习过程中,如图所示,军舰A测得潜艇C的俯角为30°,在军舰A正上方1000米的反潜直升机B测得潜艇C的俯角为68°.请根据以上数据计算潜艇的下潜深度.(结果保留整数,参考数据:sin68°≈0.9,cos68°≈0.4,tan68°≈2.5°,$\sqrt{3}$≈1.7)
我海军在我国的南海海域举行反潜实战演习.在演习过程中,如图所示,军舰A测得潜艇C的俯角为30°,在军舰A正上方1000米的反潜直升机B测得潜艇C的俯角为68°.请根据以上数据计算潜艇的下潜深度.(结果保留整数,参考数据:sin68°≈0.9,cos68°≈0.4,tan68°≈2.5°,$\sqrt{3}$≈1.7)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com