
【题目】如图,平面直角坐标系![]() 中,一次函数
中,一次函数![]() (
(![]() 为常数,
为常数,![]() )的图像与
)的图像与![]() 轴、
轴、![]() 轴分别相交于点
轴分别相交于点![]() ,半径为4的⊙
,半径为4的⊙![]() 与
与![]() 轴正半轴相交于点
轴正半轴相交于点![]() ,与
,与![]() 轴相交于点
轴相交于点![]() ,点
,点![]() 在点
在点![]() 上方.
上方.
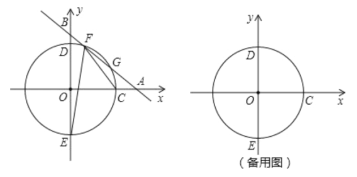
(1)若直线![]() 与弧
与弧![]() 有两个交点
有两个交点![]() .
.
①求![]() 的度数;
的度数;
②用含![]() 的代数式表示
的代数式表示![]() ,并直接写出
,并直接写出![]() 的取值范围;
的取值范围;
(2)设![]() ,在线段
,在线段![]() 上是否存在点
上是否存在点![]() ,使
,使![]() ?若存在,请求出
?若存在,请求出![]() 点坐标;若不存在,请说明理由.
点坐标;若不存在,请说明理由.
【答案】(1)①45°;②![]() ,(
,(![]() );(2)b=5时存在,点P的坐标为
);(2)b=5时存在,点P的坐标为![]() ,
,
当b>5时,直线与圆相离,不存在P,理由见解析.
【解析】
(1)连接CD,EA,利用同一条弦所对的圆周角相等求行∠CFE=45°,
(2)作OM⊥AB点M,连接OF,利用两条直线垂直相交求出交点M的坐标,利用勾股定理求出FM2,再求出FG2,再根据式子写出b的范围,
(3)当b=5时,直线与圆相切,存在点P,使∠CPE=45°,再利用△APO∽△AOB和△AMP∽△AOB相似得出点P的坐标,.
解:(1)①如图,
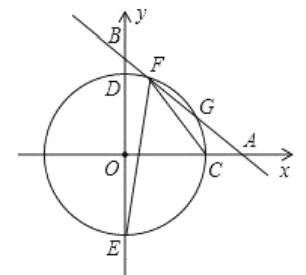
∵![]() ,
,
∴![]() ,(圆周角定理)
,(圆周角定理)
②方法一:
如图,作![]() 于
于![]() ,连接
,连接![]() ,
,
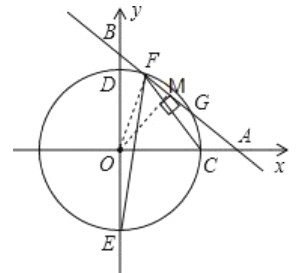
∵![]() ,直线的函数式为:
,直线的函数式为:![]() ,
,
∴![]() 所在的直线函数式为:
所在的直线函数式为:![]() ,
,
∴交点![]()
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∵直线![]() 与弧
与弧![]() 有两个交点
有两个交点![]() ,
,
∴![]() ,
,
∴![]() ,(
,(![]() )
)
方法二:
如图,作![]() 于点
于点![]() ,连接
,连接![]() ,
,
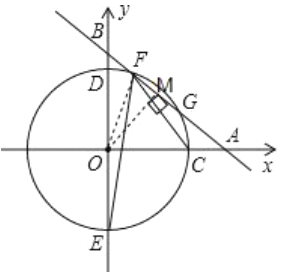
∵直线的函数式为:![]() ,
,
∴![]() 的坐标为
的坐标为![]() ,
,![]() 的坐标为
的坐标为![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴在![]() 中,
中,![]() ,
,
∵![]() ,
,
∴![]() ,
,
∵直线![]() 与弧
与弧![]() 有两个交点
有两个交点![]() ,
,
∴![]() ,
,
∴![]() ,(
,(![]() )
)
(2)如图,
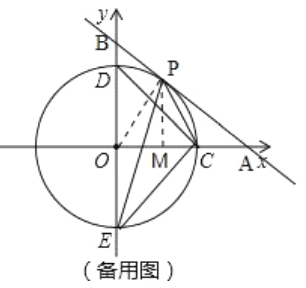
当![]() 时,直线与圆相切,
时,直线与圆相切,
∵在直角坐标系中,![]() ,
,
∴![]() ,
,
∴存在点![]() ,使
,使![]() ,
,
连接![]() ,
,
∵![]() 是切点,
是切点,
∴![]() ,
,
∴![]() ∽
∽![]() ,
,
∴![]() ,
,
∵![]() ,
,![]() ,
,![]() ,
,
∴![]() ,即
,即![]() ,
,
∵![]() ,
,
作![]() 交
交![]() 于点
于点![]() ,设
,设![]() 的坐标为
的坐标为![]() ,
,
∵![]() ∽
∽![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴点![]() 的坐标为
的坐标为![]() ,
,
当![]() 时,直线与圆相离,不存在
时,直线与圆相离,不存在![]() .
.
故答案为:(1)45°;(2)![]() ,(
,(![]() );(3)b=5时存在,点P的坐标为
);(3)b=5时存在,点P的坐标为![]() ,
,
当b>5时,直线与圆相离,不存在P,理由见解析.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
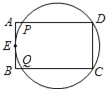
【题目】如图的矩形ABCD中,E为AB的中点,有一圆过C、D、E三点,且此圆分别与AD、BC相交于P、Q两点.甲、乙两人想找到此圆的圆心O,其作法如下:
(甲) 作∠DEC的角平分线L,作DE的中垂线,交L于O点,则O即为所求;
(乙) 连接PC、QD,两线段交于一点O,则O即为所求.
对于甲、乙两人的作法,下列判断何者正确?( )
A. 两人皆正确 B. 两人皆错误
C. 甲正确,乙错误 D. 甲错误,乙正确
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,抛物线
,抛物线![]() 经过点
经过点![]() ,
,![]() .点
.点![]() 为
为![]() 轴上一动点,过点
轴上一动点,过点![]() 且垂直于
且垂直于![]() 轴的直线分别交直线
轴的直线分别交直线![]() 及抛物线于点
及抛物线于点![]() ,
,![]() .
.
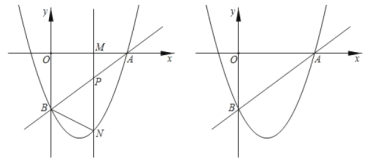
(1)填空:点![]() 的坐标为_________,抛物线的解析式为_________;
的坐标为_________,抛物线的解析式为_________;
(2)当点![]() 在线段
在线段![]() 上运动时(不与点
上运动时(不与点![]() ,
,![]() 重合),
重合),
①当![]() 为何值时,线段
为何值时,线段![]() 最大值,并求出
最大值,并求出![]() 的最大值;
的最大值;
②求出使![]() 为直角三角形时
为直角三角形时![]() 的值;
的值;
(3)若抛物线上有且只有三个点![]() 到直线
到直线![]() 的距离是
的距离是![]() ,请直接写出此时由点
,请直接写出此时由点![]() ,
,![]() ,
,![]() ,
,![]() 构成的四边形的面积.
构成的四边形的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
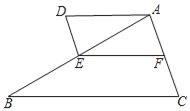
【题目】如图,已知点D在△ABC的外部,AD∥BC,点E在边AB上,ABAD=BCAE.
(1)求证:∠BAC=∠AED;
(2)在边AC取一点F,如果∠AFE=∠D,求证:![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】环保局对某企业排污情况进行检测,结果显示,所排污水中硫化物的浓度超标,即硫化物的浓度超过最高允许的![]() ,环保局要求该企业立即整改,在15天以内(含15天)排污达标,整改过程中,所排污水中硫化物的浓度
,环保局要求该企业立即整改,在15天以内(含15天)排污达标,整改过程中,所排污水中硫化物的浓度![]() 与时间
与时间![]() (天)的变化规律如图所示,其中线段
(天)的变化规律如图所示,其中线段![]() 表示前3天的变化规律,从第3天起,所排污水中硫化物的浓度
表示前3天的变化规律,从第3天起,所排污水中硫化物的浓度![]() 与时间
与时间![]() 成反比例关系
成反比例关系
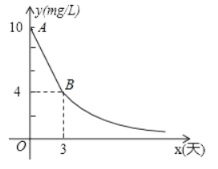
(1)求整改过程中硫化物的浓度![]() 与时间
与时间![]() 的函数表达式(要求标注自变量
的函数表达式(要求标注自变量![]() 的取值范围)
的取值范围)
(2)该企业所排污水中硫化物的浓度,能否在15天以内(含15天)排污达标?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
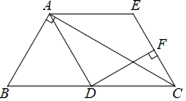
【题目】如图,在△ABC中,∠BAC=90°,点D是BC中点,AE∥BC,CE∥AD.
(1)求证:四边形ADCE是菱形;
(2)过点D作DF⊥CE于点F,∠B=60°,AB=6,求EF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】济南某中学在参加“创文明城,点赞泉城”书画比赛中,杨老师从全校30个班中随机抽取了4个班(用A,B,C,D表示),对征集到的作鼎的数量进行了分析统计,制作了两幅不完整的统计图.

请根据以上信息,回答下列问题:
(l)杨老师采用的调查方式是 (填“普查”或“抽样调查”);
(2)请补充完整条形统计图,并计算扇形统计图中C班作品数量所对应的圆心角度数 .
(3)请估计全校共征集作品的什数.
(4)如果全枝征集的作品中有5件获得一等奖,其中有3名作者是男生,2名作者是女生,现要在获得一样等奖的作者中选取两人参加表彰座谈会,请你用列表或树状图的方法,求恰好选取的两名学生性别相同的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
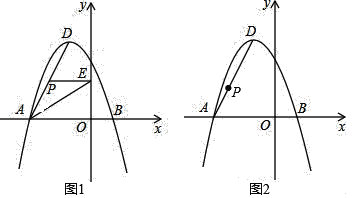
【题目】如图,在平面直角坐标系中,抛物线y=ax2+bx+3经过A(﹣3,0)、B(1,0)两点,其顶点为D,连接AD,点P是线段AD上一个动点(不与A、D重合).
(1)求抛物线的函数解析式,并写出顶点D的坐标;
(2)如图1,过点P作PE⊥y轴于点E.求△PAE面积S的最大值;
(3)如图2,抛物线上是否存在一点Q,使得四边形OAPQ为平行四边形?若存在求出Q点坐标,若不存在请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
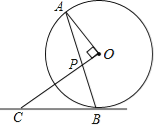
【题目】如图,AB是⊙O的弦,OP⊥OA交AB于点P,过点B的直线交OP的延长线于点C,且CP=CB.
(1)求证:BC是⊙O的切线;
(2)若⊙O的半径为![]() ,OP=1,求BC的长.
,OP=1,求BC的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com