
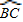 上的一动点.
上的一动点.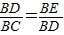 ?请说明理由;
?请说明理由;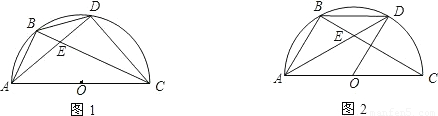
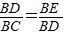 成立,则应有△BDE∽△BCD,因此必须满足∠BDE=∠DCB,则弧BD=弧AB,故需添加BD=AB;
成立,则应有△BDE∽△BCD,因此必须满足∠BDE=∠DCB,则弧BD=弧AB,故需添加BD=AB;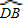 =
=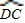 ;
;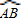 =
=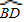 ,
,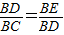 .
.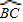 的中点.
的中点.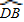 =
=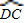 .
. =
=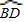 =
=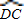 ,
,

 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案科目:初中数学 来源: 题型:
 |
| BC |
| BD |
| BC |
| BE |
| BD |
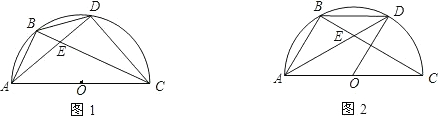
查看答案和解析>>
科目:初中数学 来源: 题型:
 | BC |
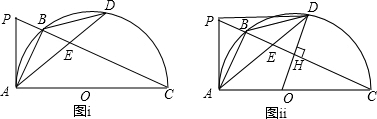 与H,BE=2,EC=4,连接PD,请探究四边形ABDO是什么特殊的四边形,并求tan∠DPC的值.
与H,BE=2,EC=4,连接PD,请探究四边形ABDO是什么特殊的四边形,并求tan∠DPC的值.查看答案和解析>>
科目:初中数学 来源:第26章《圆》常考题集(20):26.4 圆周角(解析版) 题型:解答题
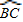 上的一动点.
上的一动点.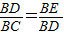 ?请说明理由;
?请说明理由;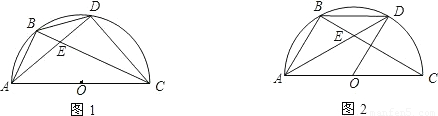
查看答案和解析>>
科目:初中数学 来源:第4章《相似三角形》常考题集(10):4.3 两个三角形相似的判定(解析版) 题型:解答题
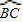 上的一动点.
上的一动点.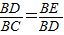 ?请说明理由;
?请说明理由;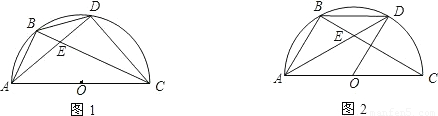
查看答案和解析>>
科目:初中数学 来源:2010年四川省成都市大邑县外国语学校中考数学模拟试卷(解析版) 题型:解答题
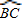 上的一动点,P在CB的延长线上,且有∠BAP=∠BDA.
上的一动点,P在CB的延长线上,且有∠BAP=∠BDA.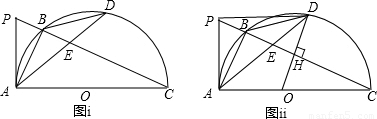
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com