
【题目】填空,将理由补充完整.
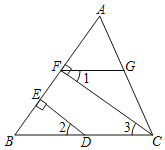
如图,CF⊥AB于F,DE⊥AB于E,∠1+∠EDC=180°,求证:FG∥BC
证明:∵CF⊥AB,DE⊥AB(已知)
∴∠BED=∠BFC=90°(垂直的定义)
∴ED∥FC ( )
∴∠2=∠3 ( )
∵∠1+∠EDC=180°(已知)
又∵∠2+∠EDC=180°(平角的定义)
∴∠1=∠2 ( )
∴∠1=∠3(等量代换)
∴FG∥BC ( )
【答案】同位角相等,两直线平行;两直线平行,同位角相等;等量代换;内错角相等,两直线平行.
【解析】
由垂直的定义得出∠BED=∠BFC=90°;由同位角相等得出ED∥FC;由两直线平行,同位角相等,得出∠2=∠3;由∠1+∠EDC=180°,∠2+∠EDC=180°,等量代换得出∠1=∠2,等量代换得出∠1=∠3;由内错角相等,两直线平行即可得出结论.
证明:∵CF⊥AB,DE⊥AB(已知),
∴∠BED=∠BFC=90°(垂直的定义),
∴ED∥FC (同位角相等,两直线平行),
∴∠2=∠3 (两直线平行,同位角相等),
∵∠1+∠EDC=180°(已知),
又∵∠2+∠EDC=180°(平角的定义),
∴∠1=∠2 (等量代换),
∴∠1=∠3(等量代换),
∴FG∥BC (内错角相等,两直线平行).
故答案为:同位角相等,两直线平行;两直线平行,同位角相等;等量代换;内错角相等,两直线平行.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】在Rt△ABC中,∠A=90°,AB=AC=![]() +2,D是边AC上的动点,BD的垂直平分线交BC于点E,连接DE,若△CDE为直角三角形,则BE的长为_____.
+2,D是边AC上的动点,BD的垂直平分线交BC于点E,连接DE,若△CDE为直角三角形,则BE的长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2018年1月25日,济南至成都方向的高铁线路正式开通,高铁平均时速为普快平均时速的4倍,从济南到成都的高铁运行时间比普快列车减少了26小时.已知济南到成都的火车行车里程约为2288千米,求高铁列车的平均时速.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“十年树木,百年树人”,教师的素养关系到国家的未来.我市某区招聘音乐教师采用笔试、专业技能测试、说课三种形式进行选拔,这三项的成绩满分均为100分,并按2:3:5的比例折合纳入总分,最后,按照成绩的排序从高到低依次录取.该区要招聘2名音乐教师,通过笔试、专业技能测试筛选出前6名选手进入说课环节,这6名选手的各项成绩见表:
序号 | 1 | 2 | 3 | 4 | 5 | 6 |
笔试成绩 | 66 | 90 | 86 | 64 | 65 | 84 |
专业技能测试成绩 | 95 | 92 | 93 | 80 | 88 | 92 |
说课成绩 | 85 | 78 | 86 | 88 | 94 | 85 |
(1)求出说课成绩的中位数、众数;
(2)已知序号为1,2,3,4号选手的成绩分别为84.2分,84.6分,88.1分,80.8分,请你判断这六位选手中序号是多少的选手将被录用?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
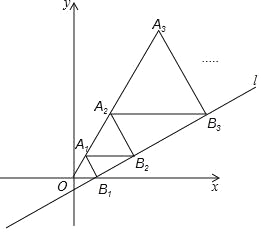
【题目】如图,在平面直角坐标系中,直线l:y=![]() x﹣
x﹣![]() 与x轴交于点B1,以OB1为边长作等边三角形A1OB1,过点A1作A1B2平行于x轴,交直线l于点B2,以A1B2为边长作等边三角形A2A1B2,过点A2作A2B3平行于x轴,交直线l于点B3,以A2B3为边长作等边三角形A3A2B3,…,则点A2017的横坐标是 .
与x轴交于点B1,以OB1为边长作等边三角形A1OB1,过点A1作A1B2平行于x轴,交直线l于点B2,以A1B2为边长作等边三角形A2A1B2,过点A2作A2B3平行于x轴,交直线l于点B3,以A2B3为边长作等边三角形A3A2B3,…,则点A2017的横坐标是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
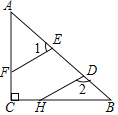
【题目】如图,D,E为△ABC边AB上两点,F,H分别在AC,BC上,∠1+∠2=180°
(1)求证:EF∥DH;
(2)若∠ACB=90°,∠DHB=25°,求∠EFC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,A(0,1),B(5,0)将线段AB向上平移到DC,如图1,CD交y轴于点E,D点坐标为(﹣2,a)
(1)直接写出点C坐标(C的纵坐标用a表示);
(2)若四边形ABCD的面积为18,求a的值;
(3)如图2,F为AE延长线上一点,H为OB延长线上一点,EP平分∠CEF,BP平分∠ABH,求∠EPB的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在正方形ABCD中,点E为BC边的中点,点B′与点B关于AE对称,B′B与AE交于点F,连接AB′,DB′,FC.下列结论:①AB′=AD;②△FCB′为等腰直角三角形;③∠ADB′=75°;④∠CB′D=135°.其中正确的是( )

A. ①② B. ①②④ C. ③④ D. ①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学开展“我的中国梦”演讲比赛活动,九(1)、九(2)班根据初赛成绩各选出5名选手参加复赛,两个班各选出的5名选手的复赛成绩(满分为100分)如下图所示.

(1)根据如图,分别求出两班复赛的平均成绩和方差;
(2)根据(1)的计算结果,分析哪个班级5名选手的复赛成绩波动小?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com