
【题目】已知:在平面直角坐标系中,点O为坐标原点,直线![]() 交x轴于点A,交y轴于点B,点D在直线AB上,点D的纵坐标为6,点C在x轴上且位于原点右侧,连接CD,且
交x轴于点A,交y轴于点B,点D在直线AB上,点D的纵坐标为6,点C在x轴上且位于原点右侧,连接CD,且![]() .
.
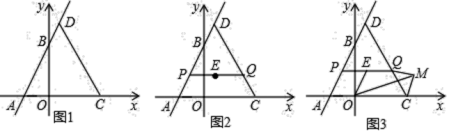
![]() 如图1,求直线CD的解析式;
如图1,求直线CD的解析式;
![]() 如图2,点P在线段AB上
如图2,点P在线段AB上![]() 点P不与点A,B重合
点P不与点A,B重合![]() ,过点P作
,过点P作![]() 轴,交CD于点Q,点E是PQ的中点,设P点的横坐标为t,EQ的长为d,求d与t之间的函数关系式,并直接写出自变量t的取值范围;
轴,交CD于点Q,点E是PQ的中点,设P点的横坐标为t,EQ的长为d,求d与t之间的函数关系式,并直接写出自变量t的取值范围;
![]() 如图3,在
如图3,在![]() 的条件下,以CQ为斜边作等腰直角
的条件下,以CQ为斜边作等腰直角![]() ,且点M在直线CD的右侧,连接OE,OM,当
,且点M在直线CD的右侧,连接OE,OM,当![]() 时,求点M的坐标.
时,求点M的坐标.
【答案】(1)![]() (2)
(2)![]() (3)
(3)![]()
【解析】
(1)A、D两点在直线y=2x+4上,可依条件建立方程求得坐标,再根据等腰三角形性质求得点C坐标,应用待定系数法求直线CD解析式;
(2)点P在线段AB上,可得P(t,2t+4),根据PQ∥x轴,可得P与Q纵坐标相等,求得Q(-t+2,2t+4),根据E为PQ中点,可得d=EQ=12PQ=-t+1;
(3)过M作SR⊥x轴于R,交PQ延长线于S,利用等腰三角形两腰相等构造全等三角形,在TQ上截取TF=OT,构造等腰Rt△TOF,应用相似三角形判定和性质,建立方程求解.
(1)如图1,
直线y=2x+4经过点A,D,
当y=0时,x=-2,
∴A(-2,0),
当y=6时,x=1,
∴D(1,6),
过点D作DL⊥x轴于点L,
∴L(1,0),
∴AL=3,
∵AD=CD,
∴AL=CL=3,
∴OC=1+3=4,
∴C(4,0),
设直线CD的解析式为y=kx+b,将C(4,0),D(1,6)代入得
![]() ,
,
解得k=-2,b=8,
∴直线CD的解析式为y=-2x+8;
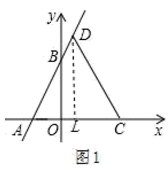
(2)如图2,过点P,Q分别作PF⊥x轴于点F,QG⊥x轴于点G,PQ交y轴于点T,
∵点P在直线y=2x+4上且点P的横坐标为t,
∴点P的坐标为(t,2t+4),
∵PQ∥z轴,
∴∠OTQ=∠AOT=90°,
∴PQ⊥y轴,
∴OT=2t+4,
∴点Q的纵坐标为2t+4,
点Q在直线y=-2x+8上,当y=2t+4时,2t+4=-2x+8,解得x=-2t+2,
∴点Q的坐标为(-t+2,2t+4),
∵∠PFC=∠QGC=90°
∴PF∥QG
又∵PQ∥FG
∴四边形PFGQ为平行四边形
∴PQ=FG=(-t+2)-t=-2t+2
∵E为PQ的中点
∴EP=EQ=![]() PQ=
PQ=![]() (-2t+2)=-t+1
(-2t+2)=-t+1
∴d=-t+1 (-1<t<0);
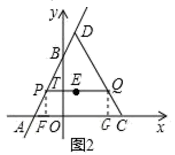
(3)如图3,过点M作x轴的垂线,垂足为R,交PQ的延长线于点S,
∵∠CMQ=90°,CM=MQ
∴∠QCM=45°
在△OCM中,∠COM+∠OMC+∠OCM=180°
∴(90°-∠BCE-∠ECM)+(90°-∠OMQ)+(∠ACD+45°)=180°
又∵∠BOE+∠OMQ=∠ACD
∴∠EOM=45
令CR=m,
∵∠OTS=∠TOR=∠ORS=90°
∴四边形ORST是矩形
∴RS=OT=2t+4,TS=OR=m+4
∴QS=m+4-(-t+2)=m+t+2
∵CM=QM,∠CRM=∠MSQ=90°,∠MCR=90°-∠CMR=∠QMS
∴△QMS≌△MCR
∴MS=CR=m,MR=QS=m+t+2
∵MS+MR=RS
∴m+m+t+2=2t+4
∴m=![]() t+1
t+1
∴MR=![]() t+3,OR=
t+3,OR=![]() t+5
t+5
在TQ上截取TF=OT=2t+4,连接OF,过点E作EH⊥OF于点H,
则∠COF=∠TFO=45°,OF=![]() OT=
OT=![]() (2t+4),EF=FT-ET=2t+4-(-t+1+t)=2t+3,EH=FH=
(2t+4),EF=FT-ET=2t+4-(-t+1+t)=2t+3,EH=FH=![]() EF=
EF=![]() (2t+3),
(2t+3),
∴OH=OF-FH=![]() (2t+4)-
(2t+4)-![]() (2t+3)=
(2t+3)=![]() (2t+5),
(2t+5),
∵∠MOR=45°-∠FOM=∠EOH
∴tan∠MOR=tan∠EOH
在Rt△MOR中,tan∠MOR=![]() ,在Rt△OEH中,tan∠EOH=
,在Rt△OEH中,tan∠EOH=![]() ,
,
∴![]()
∴MROH=OREH
∴![]()
![]()
解得![]() (舍去)
(舍去)
∴![]()
过点M作MK⊥y轴于点K,可证四边形ORMK是矩形
∴![]()
∴点M的坐标为![]() .
.


 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案科目:初中数学 来源: 题型:
【题目】已知![]() 和
和![]() 中,
中,![]() ,
,![]() ,
,![]() ,(其中
,(其中![]() ),连接
),连接![]() 、
、![]() ,点
,点![]() 为线段
为线段![]() 的中点,连接
的中点,连接![]() 、
、![]() ,
,![]() 绕点
绕点![]() 顺时针旋转,探究线段
顺时针旋转,探究线段![]() 与
与![]() 的数量关系.
的数量关系.
(1)如图1,点![]() 落在
落在![]() 边上时,探究
边上时,探究![]() 与
与![]() 的数量关系,并说明理由;
的数量关系,并说明理由;
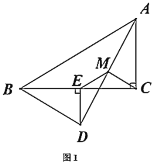
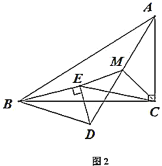
(2)如图2,点![]() 落在
落在![]() 内部时,探究
内部时,探究![]() 与
与![]() 的数量关系,并说明理由;
的数量关系,并说明理由;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:△ABC 内接于⊙O,过点 A 作⊙O 的切线交 CB 的延长线于点 P,且∠PAB=45°.
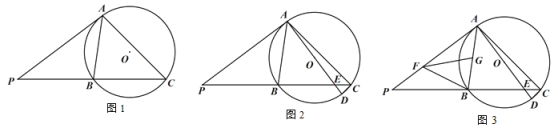
(1)如图 1,求∠ACB 的度数;
(2)如图 2,AD 是⊙O 的直径,AD 交 BC 于点 E,连接 CD,求证:AC CD ![]() ;
;
(3)如图 3 ,在(2)的条件下,当 BC 4![]() CD 时,点 F,G 分别在 AP,AB 上,连接 BF,FG,∠BFG=∠P,且 BF=FG,若 AE=15,求 FG 的长.
CD 时,点 F,G 分别在 AP,AB 上,连接 BF,FG,∠BFG=∠P,且 BF=FG,若 AE=15,求 FG 的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抗击疫情,众志成城,举国上下,共克时艰.为确定应对疫情影响稳外贸稳外资的新举措,国务院总理李克强 3 月 10 日主持召开国务院常务会议,要求更好发挥专项再贷款再贴 现政策作用,支持疫情防控保供和企业纾困发展.会议指出,近段时间,有关部门按照国务 院要求,引导金融机构实施![]() 亿元专项再贷款政策,以优惠利率资金有力支持了疫情防 控物资保供、农业和企业特别是小微企业复工复产.要进一步把政策落到位,加快贷款投放 进度,更好保障防疫物资保供、春耕备耕、国际供应链产品生产、劳动密集型产业、中小微 企业等资金需求.数据
亿元专项再贷款政策,以优惠利率资金有力支持了疫情防 控物资保供、农业和企业特别是小微企业复工复产.要进一步把政策落到位,加快贷款投放 进度,更好保障防疫物资保供、春耕备耕、国际供应链产品生产、劳动密集型产业、中小微 企业等资金需求.数据![]() 亿元用科学记数法表示为( )
亿元用科学记数法表示为( )
A.![]() 元B.
元B.![]() 元C.
元C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合与探究 如图,在平面直角坐标系中,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,抛物线
,抛物线![]() 经过
经过![]() 两点且与
两点且与![]() 轴的负半轴交于点
轴的负半轴交于点![]() .
.
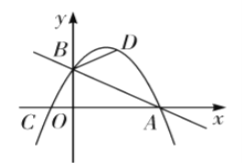
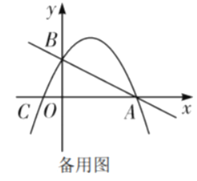
(1)求该抛物线的解析式;
(2)若![]() 为直线
为直线![]() 上方抛物线上的一个动点,当
上方抛物线上的一个动点,当![]() 时,求
时,求![]() 点的坐 标;
点的坐 标;
(3)已知![]() 分别是直线
分别是直线![]() 和抛物线上的动点,当以
和抛物线上的动点,当以![]() 为顶点的四边形 是平行四边形,且以
为顶点的四边形 是平行四边形,且以![]() 为边时,请直接写出所有符合条件的点
为边时,请直接写出所有符合条件的点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了解七、八年级学生对“防溺水”安全知识的掌握情况,从七、八年级各随机抽取50名学生进行测试,并对成绩(百分制)进行整理、描述和分析.部分信息如下:
a.七年级成绩频数分布直方图:
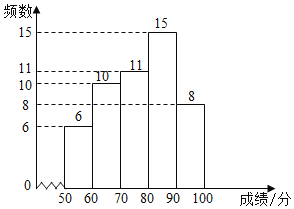
b.七年级成绩在![]() 这一组的是:70 72 74 75 76 76 77 77 77 78 79
这一组的是:70 72 74 75 76 76 77 77 77 78 79
c.七、八年级成绩的平均数、中位数如下:
年级 | 平均数 | 中位数 |
七 | 76.9 | m |
八 | 79.2 | 79.5 |
根据以上信息,回答下列问题:
(1)在这次测试中,七年级在80分以上(含80分)的有 人;
(2)表中m的值为 ;
(3)在这次测试中,七年级学生甲与八年级学生乙的成绩都是78分,请判断两位学生在各自年级的排名谁更靠前,并说明理由;
(4)该校七年级学生有400人,假设全部参加此次测试,请估计七年级成绩超过平均数76.9分的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司投入研发费用40万元(40万元只计入第一年成本),成功研发出一种产品.公司按订单生产(产量=销售量),第一年该产品正式投产后,生产成本为4元/件.此产品年销售量y(万件)与售价x(元件)之间满足函数关系式y=﹣x+20.
(1)求这种产品第一年的利润W(万元)与售价x(元件)满足的函数关系式;
(2)该产品第一年的利润为24万元,那么该产品第一年的售价是多少?
(3)第二年,该公司将第一年的利润24万元(24万元只计入第二年成本)再次投入研发,使产品的生产成本降为3元/件.为保持市场占有率,公司规定第二年产品售价不超过第一年的售价,另外受产能限制,销售量无法超过10万件.请计算该公司第二年的利润W2至少为多少万元.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知二次函数的图像过点![]() ,
,![]() ,与
,与![]() 轴交于另一点
轴交于另一点![]() ,且对称轴是直线
,且对称轴是直线![]() .
.
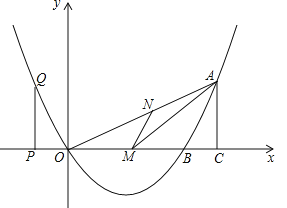
(1)求该二次函数的解析式;
(2)若![]() 是
是![]() 上的一点,作
上的一点,作![]() 交
交![]() 于
于![]() ,当
,当![]() 面积最大时,求
面积最大时,求![]() 的坐标;
的坐标;
(3)![]() 是
是![]() 轴上的点,过
轴上的点,过![]() 作
作![]() 轴,与抛物线交于
轴,与抛物线交于![]() ,过
,过![]() 作
作![]() 轴于
轴于![]() .当以
.当以![]() 、
、![]() 、
、![]() 为顶点的三角形与
为顶点的三角形与![]() 、
、![]() 、
、![]() 为顶点的三角形相似时,求
为顶点的三角形相似时,求![]() 点的坐标.
点的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com