
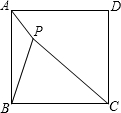
 如图,P是正方形ABCD内一点,PA=3,PB=6,PC=9.求∠APB的度数.
如图,P是正方形ABCD内一点,PA=3,PB=6,PC=9.求∠APB的度数.| 2 |
| 2 |
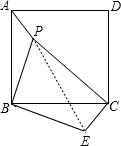 解:∵四边形ABCD为正方形,
解:∵四边形ABCD为正方形,| 2 |
| 2 |


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
| A、检测某城市的空气质量 |
| B、估计某池塘中现有鱼的数量 |
| C、某单位招聘员工,对应聘人员进行面试 |
| D、调查某种节能灯的使用寿命 |
查看答案和解析>>
科目:初中数学 来源: 题型:
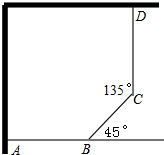 用30m长的篱笆和相邻两面墙围成如图形状的小花园,其中AB=CD.设BC=x(m),小花园的面积为S(m2).求:
用30m长的篱笆和相邻两面墙围成如图形状的小花园,其中AB=CD.设BC=x(m),小花园的面积为S(m2).求:查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
| k |
| x |
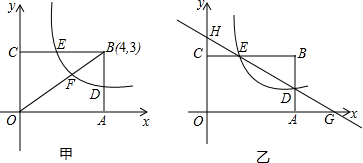
| BD |
| BE |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com