
二次函数y=﹣2(x﹣1)2+3的图象的顶点坐标是( )
A. (1,3) B. (﹣1,3) C. (1,﹣3) D. (﹣1,﹣3)
A 【解析】由二次函数顶点式知,顶点是(1,3),选A. 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案科目:初中数学 来源:江苏省南京市联合体2018届九年级上学期期末考试数学试卷 题型:填空题
若关于x的一元二次方程x2+4x+k﹣1=0有实数根,则k的取值范围是____.
k≤5 【解析】由题意得 42-4×1×(k-1)≥0, 解之得 k≤5.查看答案和解析>>
科目:初中数学 来源:北京大学附属中学2017-2018学年七年级上学期期中考试数学试卷 题型:填空题
若 ,则
,则 的值为__________.
的值为__________.
查看答案和解析>>
科目:初中数学 来源:天津市2018届九年级(上)第四周周清数学试卷 题型:解答题
已知二次函数的图象与x轴的两个交点坐标是(﹣3,0)和(4,0),这个函数也过点(6,18),求这个二次函数的解析式.
y=x2﹣x﹣12 【解析】试题分析:设二次函数的解析式为y=ax2+bx+c(a≠0),再把函数的图象与x轴的两个交点坐标以及点(6,18)代入求出a,b,c的值即可. 试题解析:设二次函数的解析式为y=ax2+bx+c(a≠0). 根据题意,得, 解得: , ∴二次函数的解析式为y=x2﹣x﹣12.查看答案和解析>>
科目:初中数学 来源:天津市2018届九年级(上)第四周周清数学试卷 题型:填空题
抛物线y=﹣2(x+1)2﹣3的开口向_____,对称轴是_____,顶点坐标是_____,当x_____时,y随x的增大而减小,当x_____时,y有最_____值,是y=_____.
下 x=﹣1 (﹣1,﹣3) x>﹣1 x=﹣1 大 -3 【解析】试题解析:抛物线y=﹣2(x+1)2﹣3的开口向下,对称轴是直线x=﹣1,顶点坐标是(﹣1,﹣3),当x>﹣1时,y随x的增大而减小,当x=﹣1时,y有最大值,是y=﹣3, 故答案为:下,x=﹣1,(﹣1,﹣3),x>﹣1,x=﹣1,大,﹣3查看答案和解析>>
科目:初中数学 来源:广东省广州市天河区2017-2018学年八年级上学期期末考试数学试卷 题型:解答题
如图,△ABC中,AB=AC,作AD⊥BC,CE⊥AB,垂足分别为D,E,AD和CE相交于点F,若已知AE=CE.
(1)求证:△AEF≌△CEB;
(2)求证:AF=2CD

查看答案和解析>>
科目:初中数学 来源:广东省广州市天河区2017-2018学年八年级上学期期末考试数学试卷 题型:填空题
如图,△AEB≌△DFC,AE⊥CB,DF⊥BC,垂足分别为E、F,且AE=DF,若∠C=28°,则∠A=__________.

查看答案和解析>>
科目:初中数学 来源:江苏省东部分校2017-2018学年八年级上学期期末考试数学试卷 题型:解答题
一次函数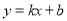 的图象过点
的图象过点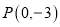 ,与函数
,与函数 的图象相交于
的图象相交于 .
.
(1)求 的值;
的值;
(2)若函数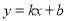 的图象与
的图象与 轴的交点是B,函数
轴的交点是B,函数 的图象与
的图象与 轴的交点是C,与x轴交于点D,求三角形ABD的面积(其中O为坐标原点).
轴的交点是C,与x轴交于点D,求三角形ABD的面积(其中O为坐标原点).
查看答案和解析>>
科目:初中数学 来源:湖南省武冈市2017-2018学年八年级上学期期末考试数学试卷 题型:单选题
一艘轮船在静水中的最大航速为30千米/时,它沿江以最大航速顺流航行100千米所用时间,与以最大航速逆流航行60千米所用时间相等,江水的流速为多少?设江水的流速为 千米/时,则可列方程( )
千米/时,则可列方程( )
A. 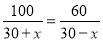 B.
B. 
C.  D.
D. 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com