
【题目】如图,平行四边形ABCD的对角线AC,BD交于点O,AE平分∠BAD交BC于点E,且∠ADC=60°,AB=![]() BC,连接OE,下列结论:①∠CAD=30°;②SABCD=ABAC;③OB=AB:④OE=
BC,连接OE,下列结论:①∠CAD=30°;②SABCD=ABAC;③OB=AB:④OE=![]() BC.其中成立的有( )
BC.其中成立的有( )

A.①②③B.①②④C.①③④D.②③④
【答案】B
【解析】
由ABCD中,∠ADC=60°,易得△ABE是等边三角形,又由AB=![]() BC,,证得①∠CAD=30°;继而证得AC⊥AB,得②SABCD=ABAC;可得OE是三角形的中位线,证得④OE=
BC,,证得①∠CAD=30°;继而证得AC⊥AB,得②SABCD=ABAC;可得OE是三角形的中位线,证得④OE=![]() BC.
BC.
解:∵四边形ABCD是平行四边形,
∴∠ABC=∠ADC=60°,∠BAD=120°,
∵AE平分∠BAD,
∴∠BAE=∠EAD=60°
∴△ABE是等边三角形,
∴AE=AB=BE,
∵AB=![]() BC,
BC,
![]() ,
,
∴∠BAC=90°,
∴∠CAD=30°,故①正确;
∵AC⊥AB,
∴SABCD=ABAC,故②正确,
![]() ,
,
∵BD>BC,
∴AB≠OB,故③错误;
∵∠CAD=30°,∠AEB=60°,AD∥BC,
∴∠EAC=∠ACE=30°,
∴AE=CE,
∴BE=CE,
∵OA=OC,
![]() ,故④正确.
,故④正确.
故选:B.


 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案科目:初中数学 来源: 题型:
【题目】某商店第一次购进相同铅笔1000支,第二次又购进同种铅笔,购进数量是第一次的![]() ,这次每支铅笔的进价比第一次进价高0.2元,第二次购进铅笔比第一次少花300元.
,这次每支铅笔的进价比第一次进价高0.2元,第二次购进铅笔比第一次少花300元.
(1)求第一次每支铅笔的进价是多少元?
(2)第一次购进铅笔在第一次进价的基础上加价50%出售;第二次购进的铅笔以每支1.5元的价格出售,出售一部分后又在每支1.5元的基础上打八折出售;两次购进的铅笔全部销售完毕后总获利为560元,问第二次购进的铅笔出售多少支后打八折出售?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】轮胎的直径是否符合标准,是判断轮胎质量的好与差的重要依据之一.东风轮胎厂某批轮胎的标准直径是![]() ,质量检验员从这批产品中抽取10个轮胎进行检查,超过标准直径的毫米数记为正,不足的毫米数记为负,检查记录如下(单位:
,质量检验员从这批产品中抽取10个轮胎进行检查,超过标准直径的毫米数记为正,不足的毫米数记为负,检查记录如下(单位:![]() ):
):

(1)若与标准直径比较相差不超过![]() 的为合格品,请用所学的数学知识说明第几号轮胎不合格?不合格轮胎的实际直径是多少毫米?
的为合格品,请用所学的数学知识说明第几号轮胎不合格?不合格轮胎的实际直径是多少毫米?
(2)若与标准直径比较相差不超过![]() 的为合格品,请根据抽查的结果估算一下这批轮胎的合格率大约是多少?
的为合格品,请根据抽查的结果估算一下这批轮胎的合格率大约是多少?
(3)求这10个轮胎的平均直径(精确到![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)特例探究.
如图(1),在等边三角形ABC中,BD是∠ABC的平分线,AE是BC边上的高线,BD和AE相交于点F.
请你探究![]() 是否成立,请说明理由;请你探究
是否成立,请说明理由;请你探究![]() 是否成立,并说明理由.
是否成立,并说明理由.
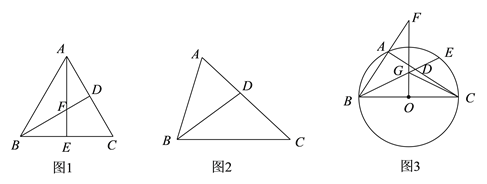
(2)归纳证明.
如图(2),若△ABC为任意三角形,BD是三角形的一条内角平分线,请问![]() 一定成立吗?并证明你的判断.
一定成立吗?并证明你的判断.
(3)拓展应用.
如图(3),BC是△ABC外接圆⊙O的直径,BD是∠ABC的平分线,交⊙O于点E,过点O作BC的垂线,交BA的延长线于点F,交BD于点G,连接CG,其中cos∠ACB=![]() ,请直接写出
,请直接写出![]() 的值;若△BGF的面积为S,请求出△COG的面积(用含S的代数式表示).
的值;若△BGF的面积为S,请求出△COG的面积(用含S的代数式表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法:
①连接两点间的线段叫这两点的距离;
②木匠师傅锯木料时,一般先在模板上画出两个点,然后过这两点弹出一条墨线,这样做的原理是:两点之间,线段最短;
③若![]() 三点在同一直线上,且
三点在同一直线上,且![]() ,则
,则![]() 是线段
是线段![]() 的中点;
的中点;
④若![]() ,则有
,则有![]() .
.
其中一定正确的是_________(把你认为正确结论的序号都填上) .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角墙角AOB(OA⊥OB,且OA、OB长度不限)中,要砌20m长的墙,与直角墙角AOB围成地面为矩形的储仓,且地面矩形AOBC的面积为96m2.
(1)求地面矩形AOBC的长;
(2)有规格为0.80×0.80和1.00×1.00(单位:m)的地板砖单价分别为55元/块和80元/块,若只选其中一种地板砖都恰好能铺满储仓的矩形地面(不计缝隙),用哪一种规格的地板砖费用较少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我国很多城市水资源缺乏,为了加强居民的节水意识,某市制定了每月用水4吨以内(包括4吨)和用水4吨以上收费标准(收费标准:每吨水的价格)某用户每月应交水费y(元)与用水量x(吨)之间关系的图象如图:
(1)说出自来水公司在这两个用水范围内的收费标准;
(2)当x>4时,求因变量y与自变量x之间的关系式;
(3)若某用户该月交水费26元,求他用了多少吨水?
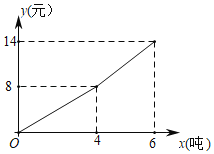
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为推进“传统文化进校园”活动,某校准备成立“经典诵读”、“传统礼仪”、“民族器乐”和“地方戏曲”等四个课外活动小组.学生报名情况如图(每人只能选择一个小组):
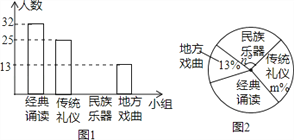
(1)报名参加课外活动小组的学生共有 人,将条形图补充完整;
(2)扇形图中m= ,n= ;
(3)根据报名情况,学校决定从报名“经典诵读”小组的甲、乙、丙、丁四人中随机安排两人到“地方戏曲”小组,甲、乙恰好都被安排到“地方戏曲”小组的概率是多少?请用列表或画树状图的方法说明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com