
分析 (1)根据题意可以利用分类讨论的数学思想列出各种情况,写出各种情况相应的方程,从而可以解答本题;
(2)根据(1)中的结果可以计算出商场的获利,然后比较大小即可解答本题;
(3)根据题意可以列出相应的三元一次方程组,注意x、y、z都是正整数,从而可以解答本题.
解答 解:(1)设学校购买甲种型号的电视机x台,购买乙种型号的电视剧y台,购买丙种型号的电视机z台,
若学校购买甲种型号的电视机和乙种型号的电视机,
$\left\{\begin{array}{l}{x+y=50}\\{1500x+2100y=90000}\end{array}\right.$,得$\left\{\begin{array}{l}{x=25}\\{y=25}\end{array}\right.$,
若学校购买甲种型号的电视机和丙种型号的电视机,
$\left\{\begin{array}{l}{x+z=50}\\{1500x+2500z=90000}\end{array}\right.$,得$\left\{\begin{array}{l}{x=35}\\{z=15}\end{array}\right.$,
若学校购买乙种型号的电视机和丙种型号的电视机,
$\left\{\begin{array}{l}{y+z=50}\\{2100y+2500z=90000}\end{array}\right.$,得$\left\{\begin{array}{l}{y=87.5}\\{z=-37.5}\end{array}\right.$(舍去),
答:学校的采购方案是购买甲种型号的电视机25台和乙种型号的电视机25台或购买甲种型号的电视机35台和丙种型号的电视机15台;
(2)当购买甲种型号的电视机25台和乙种型号的电视机25台时,
商场获利为:150×25+200×25=8750(元),
当购买甲种型号的电视机35台和丙种型号的电视机15台时,
商场获利为:150×35+250×15=9000(元),
∵8750<9000,
∴学校选择购买甲种型号的电视机25台和乙种型号的电视机25台这种方案更省钱,
答:学校选择购买甲种型号的电视机25台和乙种型号的电视机25台这种方案更省钱;
(3)设学校购买甲种型号的电视机x台,购买乙种型号的电视剧y台,购买丙种型号的电视机z台,
$\left\{\begin{array}{l}{x+y+z=50}\\{1500x+2100y+2500z=90000}\end{array}\right.$,
解得,$\left\{\begin{array}{l}{x=27}\\{y=20}\\{z=3}\end{array}\right.$或$\left\{\begin{array}{l}{x=29}\\{y=15}\\{z=6}\end{array}\right.$或$\left\{\begin{array}{l}{x=31}\\{y=10}\\{z=9}\end{array}\right.$或$\left\{\begin{array}{l}{x=33}\\{y=5}\\{z=12}\end{array}\right.$,
答:有四种购买方案,
方案一:购买甲种型号的电视机27台,购买乙种型号的电视剧20台,购买丙种型号的电视机3台,
方案二:购买甲种型号的电视机29台,购买乙种型号的电视剧15台,购买丙种型号的电视机6台,
方案三:购买甲种型号的电视机31台,购买乙种型号的电视剧10台,购买丙种型号的电视机9台,
方案四:购买甲种型号的电视机33台,购买乙种型号的电视剧5台,购买丙种型号的电视机12台.
点评 本题考查解二元一次方程组的应用、三元一次方程组的应用,解答本题的关键是明确题意,列出相应的方程,利用分类讨论的数学思想解答.


 优学名师名题系列答案
优学名师名题系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
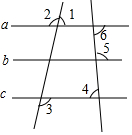 如图,下列命题是假命题的是( )
如图,下列命题是假命题的是( )| A. | 如果∠2=∠3,那么a∥c | B. | 如果a∥b,a∥c,那么b∥c | ||
| C. | 如果∠4+∠5=180°,那么∠2=∠3 | D. | 如果∠4=∠6,那么∠1+∠3=180° |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 6 | B. | 5 | C. | $12+2\sqrt{13}$ | D. | $12-2\sqrt{13}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2 018 | B. | 2 008 | C. | 2 014 | D. | 2 012 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com