
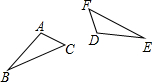
 如图,△DEF是由△ABC绕某点旋转得到,请画出这两个图形的对称中心(不写作法).
如图,△DEF是由△ABC绕某点旋转得到,请画出这两个图形的对称中心(不写作法). 科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,AB是⊙O的弦,D、E是⊙O上任意两点,连接AD,DE,AE与BD相交于点C,现给出下列四个条件:①∠ACD=∠DAB; ②AD=DE;③AD2=BD•CD; ④AD•AB=AC•BD.在以上4个条件中选取一个,能使△DAC∽△DBA的选法有( )
如图,AB是⊙O的弦,D、E是⊙O上任意两点,连接AD,DE,AE与BD相交于点C,现给出下列四个条件:①∠ACD=∠DAB; ②AD=DE;③AD2=BD•CD; ④AD•AB=AC•BD.在以上4个条件中选取一个,能使△DAC∽△DBA的选法有( )| A. | 1种 | B. | 2种 | C. | 3种 | D. | 4种 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
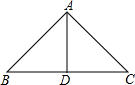 如图,如果AD是BC边上的高,又是∠BAC的平分线,那么△ABD≌△ACD,其根据是ASA;如果AD是BC边上的高,又是BC边上的中线,那么△ABD≌△ACD,其根据是SAS.
如图,如果AD是BC边上的高,又是∠BAC的平分线,那么△ABD≌△ACD,其根据是ASA;如果AD是BC边上的高,又是BC边上的中线,那么△ABD≌△ACD,其根据是SAS.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 利用一面墙(墙EF最长可利用25米),用砌37米长的墙的材料围成一个矩形花园ABCD,与围墙平行的一边BC上要预留3米宽的入口(如图中MN所示,不用砌墙).设边AB的长是x米,矩形花园ABCD的面积是y平方米.
利用一面墙(墙EF最长可利用25米),用砌37米长的墙的材料围成一个矩形花园ABCD,与围墙平行的一边BC上要预留3米宽的入口(如图中MN所示,不用砌墙).设边AB的长是x米,矩形花园ABCD的面积是y平方米.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com