
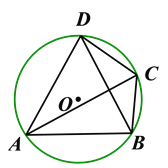
【题目】如图,在⊙O的内接四边形ABCD中,∠BCD=120°,AC平分∠BCD.
(1)求证:△ABD是等边三角形;
(2)若BD=6cm,求⊙O的半径.
【答案】(1)证明见解析;(2)![]() .
.
【解析】【试题分析】(1)因为AC平分∠BCD,∠BCD=120°, 根据角平分线的定义得:∠ACD=∠ACB=60°. 根据同弧所对的圆周角相等,得∠ACD=∠ABD, ∠ACB=∠ADB , ∠ABD=∠ADB=60°.根据三个角是60度的三角形是等边三角形得,△ABD是等边三角形.
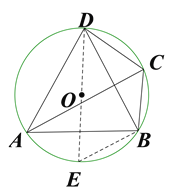
(2)作直径DE,连结BE ,由于△ABD是等边三角形,则∠BAD=60°同弧所对的圆周角相等,得∠BED=∠BAD=60°.因为DE是直径,根据直径所对的圆周角是直角得,∠EBD=90°.
则∠EDB=30°,30度所对的直角边是斜边的一半,得DE=2BE .
设EB=x,则ED=2x,根据勾股定理得,(2x)2-x2=62.
解得: ![]() ,即
,即![]() .
.
【试题解析】
(1)∵AC平分∠BCD,∠BCD=120° ,
∴∠ACD=∠ACB=60°.
∵∠ACD=∠ABD, ∠ACB=∠ADB .
∴∠ABD=∠ADB=60°.
∴△ABD是等边三角形.
(2)作直径DE,连结BE
∵△ABD是等边三角形,
∴∠BAD=60°
∴∠BED=∠BAD=60°
∵DE是直径,
∴∠EBD=90°.
∴∠EDB=30°.
∴DE=2BE .
设EB=x,则ED=2x,
∴(2x)2-x2=62.
∵x>0.
∴![]() .
.
∴![]()
即![]() .
.


 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案科目:初中数学 来源: 题型:
【题目】(1)等腰三角形一腰上的中线将这个等腰三角形的周长分成15 cm和6 cm两部分.求等腰三角形的底边长.

(2)已知等腰三角形中,有一个角比另一个角的2倍少20°,求顶角的度数
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店第一次用600元购进2B铅笔若干支,第二次又用600元购进该款铅笔,但这次每支的进价是第一次进价的![]() 倍,购进数量比第一次少了30支.
倍,购进数量比第一次少了30支.
(1)求第一次每支铅笔的进价是多少元?
(2)若要求这两次购进的铅笔按同一价格全部销售完毕后获利不低于420元,问每支售价至少是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明和同桌小聪在课后复习时,对下面的一道思考题进行了认真的探索.
【思考题】如图,一架2.5米长的梯子AB斜靠在竖直的墙AC上,这时点B到墙AC的距离为0.7米,如果梯子的顶端沿墙下滑0.4米,那么点B将向外移动________米.
解完【思考题】后,小聪提出了如下两个问题:
(1)在【思考题】中,将“下滑0.4米”改为“下滑0.9米”,那么该题的答案会是0.9米吗?为什么?
(2)在【思考题】中,梯子的顶端从A处沿墙AC下滑的距离与点B向外移动的距离,有可能相等吗?为什么?
请你解答小聪提出的这两个问题.

查看答案和解析>>
科目:初中数学 来源: 题型:
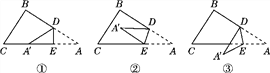
【题目】△ABC是一个三角形的纸片,点D,E分别是△ABC边AB,AC上的两点.
(1)如图①,如果沿直线DE折叠,则∠BDA′与∠A的关系是____________;
(2)如果折成图②的形状,猜想∠BDA′,∠CEA′和∠A的关系,并说明理由;
(3)如果折成图③的形状,猜想∠BDA′,∠CEA′和∠A的关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
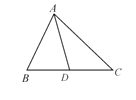
【题目】如图所示,AD是△ABC的边BC的中线.
(1)画出以点D为对称中心,与△ABD成中心对称的三角形;
(2)若AB=10,AC=12,求AD长的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料:
解答“已知![]() ,且
,且![]() ,
,![]() ,确定
,确定![]() 的取值范围”有如下解,
的取值范围”有如下解,
解:∵![]() ,
,
∴![]() .
.
又∵![]() ,
,
∴![]() .
.
∴![]() .
.
又∵![]() ,
,
∴![]() ,
,![]() ①
①
同理得:![]() .
.![]() ②
②
由①![]() ②得
②得![]() .
.
∴![]() 的取值范围是
的取值范围是![]() .
.
请按照上述方法,完成下列问题:
(![]() )已知
)已知![]() ,且
,且![]() ,
,![]() ,求
,求![]() 的取值范围.
的取值范围.
(![]() )已知
)已知![]() ,
,![]() ,若
,若![]() ,且
,且![]() ,求
,求![]() 得取值范围(结果用含
得取值范围(结果用含![]() 的式子表示).
的式子表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
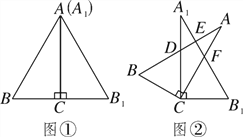
【题目】将两块相同的含30°角的直角三角板按图①的方式放置,已知∠BAC=∠B1A1C=30°,AB=2BC.固定三角板A1B1C,然后将三角板ABC绕点C顺时针方向旋转至图②的位置,AB与A1C、A1B1分别交于点D、E,AC与A1B1交于点F.
(1)当旋转角等于20°时,∠BCB1=________度;
(2)当旋转角等于多少度时,AB与A1B1垂直?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,在△ABC中,∠ABC与∠ACB的平分线相交于点P.
(1)如果∠A=80°,求∠BPC的度数;
(2)如图②,作△ABC外角∠MBC,∠NCB的角平分线交于点Q,试探索∠Q、∠A之间的数量关系.
(3)如图③,延长线段BP、QC交于点E,△BQE中,存在一个内角等于另一个内角的2倍,求∠A的度数.


查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com