
【题目】在求两位数的平方时,可以用完全平方式及“列竖式”的方法进行速算,求解过程如下.
例如:求322.
解:因为(3x+2y)2=9x2+4y2+12xy,将上式中等号右边的系数填入下面的表格中可得:
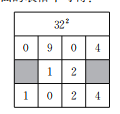
所以322=1024.
(1)下面是嘉嘉仿照例题求892的一部分过程,请你帮他填全表格及最后结果;
解:因为(8x+9y)2=64x2+81y2+144xy,将上式中等号右边的系数填入下面的表格中可得:
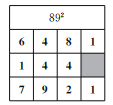
所以892= ;
(2)仿照例题,速算672;
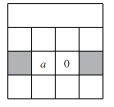
(3)琪琪用“列竖式”的方法计算一个两位数的平方,部分过程如图所示.若这个两位数的个位数字为a,则这个两位数为 (用含a的代数式表示).
【答案】(1)7921;(2)4489;(3)a+50
【解析】
(1)观察图形仿照例题即可得出答案;
(2)由(1)可得表格中第一行前面两个数为第一个数的平方,后面两个数为第二个数的平方,第二行为两数乘积的两倍,第三行把第一和第二行对应数相加即可得出答案;
(3)设这个两位数的十位数字为b,根据图利用十位数字和个位数字乘积的两个的关系列出方程用a表示b,即可得出答案.
解:(1)根据图可得:892=7921
(2)因为(6x+7y)2=36x2+49y2+84xy,将上式中等号右边的系数填入下面的表格中可得:
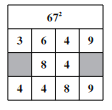
所以672=4 489.
(3)设这个两位数的十位数字为b
由题意得2ab=10a,解得b=5
所以这个两位数为10×5+a=a+50
故答案为:a+50.


 教学练新同步练习系列答案
教学练新同步练习系列答案 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线![]() 与x轴、y轴分别交于A、B两点,点P从点A出发,沿折线AB﹣BO向终点O运动,在AB上以每秒5个单位长度的速度运动,在BO上以每秒3个单位长度的速度运动;点Q从点O出发,沿OA方向以每秒
与x轴、y轴分别交于A、B两点,点P从点A出发,沿折线AB﹣BO向终点O运动,在AB上以每秒5个单位长度的速度运动,在BO上以每秒3个单位长度的速度运动;点Q从点O出发,沿OA方向以每秒![]() 个单位长度的速度运动.P,Q两点同时出发,当点P停止时,点Q也随之停止.过点P作PE⊥AO于点E,以PE,EQ为邻边作矩形PEQF,设矩形PEQF与△ABO重叠部分图形的面积为S,点P运动的时间为t秒.
个单位长度的速度运动.P,Q两点同时出发,当点P停止时,点Q也随之停止.过点P作PE⊥AO于点E,以PE,EQ为邻边作矩形PEQF,设矩形PEQF与△ABO重叠部分图形的面积为S,点P运动的时间为t秒.
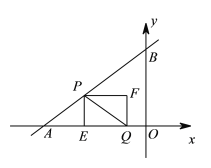
(1)连结PQ,当PQ与△ABO的一边平行时,求t的值;
(2)求S与t之间的函数关系式,并直接写出自变量t的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A,B的坐标分别为(1,4)和(4,4),抛物线y=a(x+m)2+n的顶点在线段AB上,与x轴交于C,D两点(C在D的左侧),点C的横坐标最小值为﹣3,则点D的横坐标的最大值为_____.
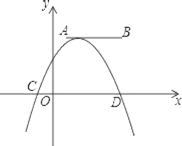
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面是“用三角板画圆的切线”的画图过程.
如图1,已知圆上一点A,画过A点的圆的切线.
![]()

画法:(1)如图2,将三角板的直角顶点放在圆上任一点C(与点A不重合)处,使其一直角边经过点A,另一条直角边与圆交于B点,连接AB;
(2)如图3,将三角板的直角顶点与点A重合,使一条直角边经过点B,画出另一条直角边所在的直线AD.
所以直线AD就是过点A的圆的切线.
请回答:该画图的依据是_______________________________________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,ΔABC中,AB=AC,∠A=40O,延长AC到D,使CD=BC,点P是ΔABD的内心,则∠BPC=

A. 105° B. 110° C. 130° D. 145°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某小区将生活垃圾分为可回收、厨余和其它三类,分别记为a,b,c,并设置了相应的垃圾箱,“可回收物”箱、“厨余垃圾”箱和“其他垃圾”箱,分别记为A,B,C.
(1)某天,小明把垃圾分装在三个袋中,可他在投放时粗心,每袋垃圾都放错了位置(每个箱中只投放一袋),请你用画树状图或列表法求小明把每袋垃圾都放错的概率;
(2)为调查居民生活垃圾分类投放情况,现随机抽取了该小区三类垃圾箱中总1000吨生活垃圾,数据统计如下(单位:吨);
A | B | C | |
a | 240 | 30 | 30 |
b | 100 | 400 | 100 |
c | 20 | 20 | 60 |
试估计“可回收物”投放正确的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数![]() 的图象与
的图象与![]() 轴交于
轴交于![]() 、
、![]() 两点,与
两点,与![]() 轴交于
轴交于![]() 点,且对称轴为直线
点,且对称轴为直线![]() ,点
,点![]() 坐标为
坐标为![]() .则下面的四个结论:①
.则下面的四个结论:①![]() ;②
;②![]() ;③
;③![]() ;④当
;④当![]() 时,
时,![]() 或
或![]() .其中正确的是( )
.其中正确的是( )

A.①②B.①③C.①④D.②③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,A、B两点的坐标分别是(8,0)、(0,6),点P由点B出发沿BA方向向点A作匀速直线运动,速度为每秒3个单位长度,点Q由A出发沿AO(O为坐标原点)方向向点O作匀速直线运动,速度为每秒2个单位长度,连接PQ,若设运动时间为t(0<t<![]() )秒.解答如下问题:
)秒.解答如下问题:
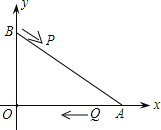
(1)当t为何值时,PQ∥BO?
(2)设△AQP的面积为S,
①求S与t之间的函数关系式,并求出S的最大值;
②若我们规定:点P、Q的坐标分别为(x1,y1),(x2,y2),则新坐标(x2﹣x1,y2﹣y1)称为“向量PQ”的坐标.当S取最大值时,求“向量PQ”的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,边长为1的正方形OA1B1C1的两边在坐标轴上,以它的对角线OB1为边作正方形OB1B2C2,再以正方形OB1B2C2的对角线OB2为边作正方形OB2B3C3,以此类推…则正方形OB2015B2016C2016的顶点B2016的坐标是______.
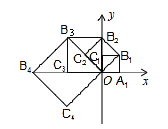
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com