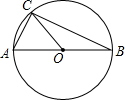
如图.AB是⊙O的直径.点C是圆上一点.∠BAC=70°.则∠OCB为( )A．70°B．20°C．140°D．35° 题目和参考答案——青夏教育精英家教网—

精英家教网 > 初中数学 > 题目详情

1．

如图，AB是⊙O的直径，点C是圆上一点，∠BAC=70°，则∠OCB为（　　）

A．

70°

B．

20°

C．

140°

D．

35°

分析由AB是⊙O的直径，根据直径所对的圆周角是直角，可求得∠ACB=90°，继而求得∠B的度数，然后由OB=OC，即可求得答案．

解答解：∵AB是⊙O的直径，
∴∠ACB=90°，
∵∠BAC=70°，
∴∠B=90°-∠BAC=20°，
∵OB=OC，
∴∠OCB=∠B=20°．
故选B．

点评此题考查了圆周角定理以及等腰三角形的性质．注意掌握直径所对的圆周角是直角定理的应用．

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：初中数学 来源： 题型：解答题

11．

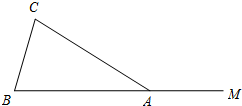如图，在△ABC中，AB=AC，点M在BA的延长线上．
（1）按下列要求作图，并在图中标明相应的字母．
①作∠CAM的平分线AN；
②作AC的中点O，连接BO，并延长BO交AN于点D，连接CD．
（2）在（1）的条件下，判断四边形ABCD的形状．并证明你的结论．

查看答案和解析>>

科目：初中数学 来源： 题型：解答题

12．计算：2^-1+$\sqrt{3}$•cos60°-（π+2015）⁰．

查看答案和解析>>

科目：初中数学 来源： 题型：解答题

9．某农业观光园计划将一块面积为900m²的园圃分成A，B，C三个区域，分别种植甲、乙、丙三种花卉，且每平方米栽种甲3株或乙6株或丙12株．已知B区域面积是A区域面积的2倍．设A区域面积为x（m²）．
（1）求该园圃栽种的花卉总株数y关于x的函数表达式．
（2）若三种花卉共栽种6600株，则A，B，C三个区域的面积分别是多少？
（3）若三种花卉的单价（都是整数）之和为45元，且差价均不超过10元，在（2）的前提下，全部栽种共需84000元．请写出甲、乙、丙三种花卉中，种植面积最大的花卉总价．

查看答案和解析>>

科目：初中数学 来源： 题型：解答题

16．

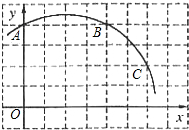如图，已知直角坐标系中一条圆弧经过正方形网格的格点A、B、C．
（1）用直尺和圆规画出该圆弧所在圆的圆心M的位置（不用写作法，保留作图痕迹）．
（2）若A点的坐标为（0，4），C点的坐标为（6，2）连接MA、MC，求扇形AMC的面积．
（3）在（2）的条件下，将扇形AMC卷成一个圆锥，求此圆锥的高．

查看答案和解析>>

科目：初中数学 来源： 题型：解答题

6．

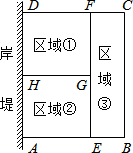为了节省材料，某水产养殖户利用水库的岸堤（岸堤足够长）为一边，用总长为80m的围网在水库中围成了如图所示的①②③三块矩形区域，而且这三块矩形区域的面积相等．设BC的长度为xm，矩形区域ABCD的面积为ym²．
（1）求y与x之间的函数关系式，并注明自变量x的取值范围；
（2）x为何值时，y有最大值？最大值是多少？

查看答案和解析>>

科目：初中数学 来源： 题型：选择题

13．

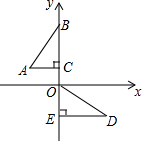如图，在平面直角坐标系中，点B、C、E、在y轴上，Rt△ABC经过变换得到Rt△ODE．若点C的坐标为（0，1），AC=2，则这种变换可以是（　　）

	A．	△ABC绕点C顺时针旋转90°，再向下平移3
	B．	△ABC绕点C顺时针旋转90°，再向下平移1
	C．	△ABC绕点C逆时针旋转90°，再向下平移1
	D．	△ABC绕点C逆时针旋转90°，再向下平移3

查看答案和解析>>

科目：初中数学 来源： 题型：解答题

10．

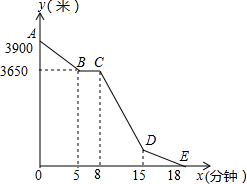小丽的家和学校在一条笔直的马路旁，某天小丽沿着这条马路上学，先从家步行到公交站台甲，再乘车到公交站台乙下车，最后步行到学校（在整个过程中小丽步行的速度不变），图中折线ABCDE表示小丽和学校之间的距离y（米）与她离家时间x（分钟）之间的函数关系．
（1）求小丽步行的速度及学校与公交站台乙之间的距离；
（2）当8≤x≤15时，求y与x之间的函数关系式．

查看答案和解析>>

科目：初中数学 来源： 题型：选择题

11．实数a，b，c，d在数轴上的对应点的位置如图所示，这四个数中，绝对值最大的是（　　）

A．

B．

C．

D．

查看答案和解析>>

同步练习册答案

练习册

高中

初中

小学