
ЁОЬтФПЁПЮЊСЫЬсИпбЇЩњЪщаДККзжЕФФмСІЃЌдіЧПБЃЛЄККзжЕФвтЪЖЃЌЮвЪаОйАьСЫЪзНьЁАККзжЬ§аДДѓШќЁБЃЌОбЁАЮКѓга50УћбЇЩњВЮМгОіШќЃЌет50УћбЇЩњЭЌЪБЬ§аД50ИіККзжЃЌШєУПе§ШЗЬ§аДГівЛИіККзжЕУ1ЗжЃЌИљОнВтЪдГЩМЈЛцжЦГіВПЗжЦЕЪ§ЗжВМБэКЭВПЗжЦЕЪ§ЗжВМжБЗНЭМШчЭМБэЃК
зщБ№ | ГЩМЈxЗж | ЦЕЪ§ЃЈШЫЪ§ЃЉ |
Ек1зщ | 25ЁмxЃМ30 | 4 |
Ек2зщ | 30ЁмxЃМ35 | 8 |
Ек3зщ | 35ЁмxЃМ40 | 16 |
Ек4зщ | 40ЁмxЃМ45 | a |
Ек5зщ | 45ЁмxЃМ50 | 10 |
ЧыНсКЯЭМБэЭъГЩЯТСаИїЬтЃК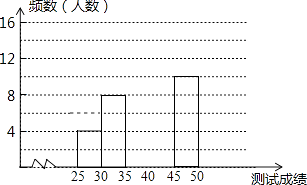
ЃЈ1ЃЉЧѓБэжаaЕФжЕЃЛ
ЃЈ2ЃЉЧыАбЦЕЪ§ЗжВМжБЗНЭМВЙГфЭъећЃЛ
ЃЈ3ЃЉШєВтЪдГЩМЈВЛЕЭгк40ЗжЮЊгХауЃЌдђБОДЮВтЪдЕФгХауТЪЪЧЖрЩйЃП
ЃЈ4ЃЉЕк5зщ10УћЭЌбЇжаЃЌга4УћФаЭЌбЇЃЌЯжНЋет10УћЭЌбЇЦНОљЗжГЩСНзщНјааЖдПЙСЗЯАЃЌЧв4УћФаЭЌбЇУПзщЗжСНШЫЃЌЧѓаЁгюгыаЁЧПСНУћФаЭЌбЇФмЗждкЭЌвЛзщЕФИХТЪЃЎ
ЁОД№АИЁП
ЃЈ1ЃЉНтЃКБэжаaЕФжЕЪЧЃК
a=50Љ4Љ8Љ16Љ10=12
ЃЈ2ЃЉНтЃКИљОнЬтвтЛЭМШчЯТЃК

ЃЈ3ЃЉНтЃКБОДЮВтЪдЕФгХауТЪЪЧ ![]() =0.44ЃЎ
=0.44ЃЎ
Д№ЃКБОДЮВтЪдЕФгХауТЪЪЧ0.44
ЃЈ4ЃЉНтЃКгУAБэЪОаЁгюЃЌBБэЪОаЁЧПЃЌCЁЂDБэЪОЦфЫћСНУћЭЌбЇЃЌИљОнЬтвтЛЪїзДЭМШчЯТЃК
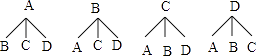
ЙВга12жжЧщПіЃЌаЁгюгыаЁЧПСНУћФаЭЌбЇЗждкЭЌвЛзщЕФЧщПіга2жжЃЌ
дђаЁгюгыаЁЧПСНУћФаЭЌбЇЗждкЭЌвЛзщЕФИХТЪЪЧ ![]()
ЁОНтЮіЁПЃЈ1ЃЉгУзмШЫЪ§МѕШЅЕк1ЁЂ2ЁЂ3ЁЂ5зщЕФШЫЪ§ЃЌМДПЩЧѓГіaЕФжЕЃЛЃЈ2ЃЉИљОнЃЈ1ЃЉЕУГіЕФaЕФжЕЃЌВЙШЋЭГМЦЭМЃЛЃЈ3ЃЉгУГЩМЈВЛЕЭгк40ЗжЕФЦЕЪ§ГЫвдзмЪ§ЃЌМДПЩЕУГіБОДЮВтЪдЕФгХауТЪЃЛЃЈ4ЃЉгУAБэЪОаЁгюЃЌBБэЪОаЁЧПЃЌCЁЂDБэЪОЦфЫћСНУћЭЌбЇЃЌЛГіЪїзДЭМЃЌдйИљОнИХТЪЙЋЪНСаЪНМЦЫуМДПЩЃЎ
ЁОПМЕуОЋЮіЁПНтД№ДЫЬтЕФЙиМќдкгкРэНтЦЕЪ§ЗжВМжБЗНЭМЕФЯрЙижЊЪЖЃЌеЦЮеЬиЕуЃКЂйвзгкЯдЪОИїзщЕФЦЕЪ§ЗжВМЧщПіЃЛЂквзгкЯдЪОИїзщЕФЦЕЪ§ВюБ№ЃЎЃЈзЂвтЧјЗжЬѕаЮЭГМЦЭМгыЦЕЪ§ЗжВМжБЗНЭМЃЉЃЌвдМАЖдСаБэЗЈгыЪїзДЭМЗЈЕФРэНтЃЌСЫНтЕБвЛДЮЪдбщвЊЩшМЦШ§ИіЛђИќЖрЕФвђЫиЪБЃЌгУСаБэЗЈОЭВЛЗНБуСЫЃЌЮЊСЫВЛжиВЛТЉЕиСаГіЫљгаПЩФмЕФНсЙћЃЌЭЈГЃВЩгУЪїзДЭМЗЈЧѓИХТЪЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПМЦЫуЃКЉ14+ЃЈ2016ЉІаЃЉ0ЉЃЈЉ ![]() ЃЉЉ1+|1Љ
ЃЉЉ1+|1Љ ![]() |Љ2sin60ЁуЃЎ
|Љ2sin60ЁуЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГЕЅЮЛгћДгФкВПеаЦИЙмРэШЫдБвЛУћЃЌЖдМзЁЂввЁЂБћШ§УћКђбЁШЫНјааСЫБЪЪдКЭУцЪдСНЯюВтЪдЃЌШ§ШЫЕФВтЪдГЩМЈШчЯТБэЫљЪОЃК
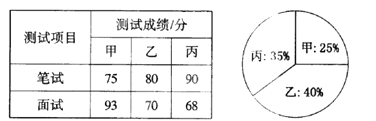
ИљОнТМгУГЬађЃЌзщжЏ200УћжАЙЄЖдШ§ШЫРћгУЭЖЦБЭЦМіЕФЗНЪННјааУёжїЦРвщЃЌШ§ШЫЕУЦБТЪЃЈУЛгаЦњШЈЦБЃЌУПЮЛжАЙЄжЛФмЭЦМі1ШЫЃЉШчЩЯЭМЫљЪОЃЌУПЕУвЛЦБМЧзї1ЗжЃЎ
ЃЈlЃЉЧыЫуГіШ§ШЫЕФУёжїЦРвщЕУЗжЃЛ
ЃЈ2ЃЉШчЙћИљОнШ§ЯюВтЪдЕФЦНОљГЩМЈШЗЖЈТМгУШЫбЁЃЌФЧУДЫНЋБЛТМгУЃЈОЋШЗЕН 0.01 )?
ЃЈ3ЃЉИљОнЪЕМЪашвЊЃЌЕЅЮЛНЋБЪЪдЁЂУцЪдЁЂУёжїЦРвщШ§ЯюВтЪдЕУЗжАД 4 : 3 : 3 ЕФБШР§ШЗЖЈИіШЫГЩМЈЃЌФЧУДЫНЋБЛТМгУЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЁїABCжаЃЌЁЯC=90ЁуЃЌADЦНЗжЁЯCABЃЌНЛCBгкЕуDЃЌЙ§ЕуDзїDEЁЭABгкЕуEЃЎ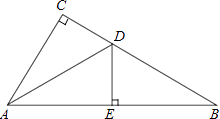
ЃЈ1ЃЉЧѓжЄЃКЁїACDЁеЁїAEDЃЛ
ЃЈ2ЃЉШєЁЯB=30ЁуЃЌCD=1ЃЌЧѓBDЕФГЄЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЗНИёжНжаУПИіаЁЗНИёЖМЪЧБпГЄЮЊ1ИіЕЅЮЛГЄЖШЕФе§ЗНаЮЃЌдкНЈСЂЦНУцжБНЧзјБъЯЕКѓЃЌЈSABCЕФЖЅЕудкИёЕуЩЯЁЃ ЧвAЃЈ1ЃЌ-4ЃЉЃЌBЃЈ5ЃЌ-4ЃЉЃЌCЃЈ4ЃЌ-1ЃЉ
ЁО1ЁПЛГіЈSABCЃЛ
ЁО1ЁПЧѓГіЈSABC ЕФУцЛ§ЃЛ![]()
ЁО1ЁПШєАбЈSABCЯђЩЯЦНвЦ2ИіЕЅЮЛГЄЖШЃЌдйЯђзѓЦНвЦ4ИіЕЅЮЛГЄЖШЕУЕНЈS![]()
![]() B
B![]() C
C![]() ЃЌдкЭМжаЛГіЈS
ЃЌдкЭМжаЛГіЈS![]()
![]() B
B![]() C
C![]() ЃЌВЂаДГіB
ЃЌВЂаДГіB![]() ЕФзјБъЁЃ
ЕФзјБъЁЃ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЖдгквЛДЮКЏЪ§y=-2x+4ЃЌЯТСаНсТлДэЮѓЕФЪЧ(ЁЁЁЁ)
A. КЏЪ§ЕФЭМЯѓгыxжсЕФНЛЕузјБъЪЧ![]()
B. КЏЪ§жЕЫцздБфСПЕФдіДѓЖјМѕаЁ
C. КЏЪ§ЕФЭМЯѓВЛОЙ§ЕкШ§ЯѓЯо
D. КЏЪ§ЕФЭМЯѓЯђЯТЦНвЦ4ИіЕЅЮЛГЄЖШЕУ![]() ЕФЭМЯѓ
ЕФЭМЯѓ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГаЁЧјЮЊСЫТЬЛЏЛЗОГЃЌМЦЛЎЗжСНДЮЙКНјAЃЌBСНжжЛЈВнЃЌЕквЛДЮЗжБ№ЙКНјAЃЌBСНжжЛЈВн30ПУКЭ15ПУЃЌЙВЛЈЗб675дЊЃЛЕкЖўДЮЗжБ№ЙКНјAЃЌBСНжжЛЈВн12ПУКЭ5ПУЃЌЙВЛЈЗб265дЊЃЈСНДЮЙКНјЕФAЁЂBСНжжЛЈВнМлИёОљЗжБ№ЯрЭЌЃЉЃЎ
ЃЈ1ЃЉAЃЌBСНжжЛЈВнУППУЕФМлИёЗжБ№ЪЧЖрЩйдЊЃП
ЃЈ2ЃЉШєЙКТђAЃЌBСНжжЛЈВнЙВ31ПУЃЌЧвBжжЛЈВнЕФЪ§СПЩйгкAжжЛЈВнЕФЪ§СПЕФ2БЖЃЌЧыФуЩшМЦвЛжжЗбгУзюЪЁЕФЗНАИЃЌВЂЧѓГіИУЗНАИЫљашЗбгУЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
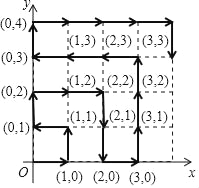
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌгаШєИЩИіКсЁЂзнзјБъЮЊећЪ§ЕФЕуЃЌЦфЫГађАДЭМжаЁАЁњЁБЗНЯђХХСаЃЌДгдЕуПЊЪМвРДЮЮЊЃЈ0ЃЌ0ЃЉЃЌЃЈ1ЃЌ0ЃЉЃЌЃЈ1ЃЌ1ЃЉЃЌЃЈ0ЃЌ1ЃЉЃЌЃЈ0ЃЌ2ЃЉЃЌЃЈ1ЃЌ2ЃЉЃЌЃЈ2ЃЌ2ЃЉЃЌЃЈ2ЃЌ1ЃЉЃЌЃЈ2ЃЌ0ЃЉЃЈ3ЃЌ0ЃЉЁАДДЫЙцТЩЕк200ИіЕуЕФзјБъЪЧ_____ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЙлВьЯТСаСНИіЕШЪНЃК![]() ЃЌ
ЃЌ![]() ЃЌИјГіЖЈвхШчЯТЃКЮвУЧГЦЪЙЕШЪН
ЃЌИјГіЖЈвхШчЯТЃКЮвУЧГЦЪЙЕШЪН ![]() ГЩСЂЕФвЛЖдгаРэЪ§
ГЩСЂЕФвЛЖдгаРэЪ§![]() ЃЌ
ЃЌ![]() ЮЊЁАЙВЩњгаРэЪ§ЖдЁБЃЌМЧЮЊЃЈ
ЮЊЁАЙВЩњгаРэЪ§ЖдЁБЃЌМЧЮЊЃЈ![]() ЃЌ
ЃЌ![]() ЃЉЃЌШчЃКЪ§ЖдЃЈ
ЃЉЃЌШчЃКЪ§ЖдЃЈ![]() ЃЌ
ЃЌ![]() ЃЉЃЌЃЈ
ЃЉЃЌЃЈ![]() ЃЌ
ЃЌ![]() ЃЉЃЌЖМЪЧЁАЙВЩњгаРэЪ§ЖдЁБЃЎ
ЃЉЃЌЖМЪЧЁАЙВЩњгаРэЪ§ЖдЁБЃЎ
ЃЈ1ЃЉЪ§ЖдЃЈ![]() ЃЌ
ЃЌ![]() ЃЉЃЌЃЈ
ЃЉЃЌЃЈ![]() ЃЌ
ЃЌ![]() ЃЉжаЪЧЁАЙВЩњгаРэЪ§ЖдЁБТ№ЃПЫЕУїРэгЩЃЎ
ЃЉжаЪЧЁАЙВЩњгаРэЪ§ЖдЁБТ№ЃПЫЕУїРэгЩЃЎ
ЃЈ2ЃЉШєЃЈ![]() ЃЌ
ЃЌ![]() ЃЉЪЧЁАЙВЩњгаРэЪ§ЖдЁБЃЌдђЃЈ
ЃЉЪЧЁАЙВЩњгаРэЪ§ЖдЁБЃЌдђЃЈ![]() ЃЌ
ЃЌ![]() ЃЉЪЧЁАЙВЩњгаРэЪ§ЖдЁБТ№ЃПЫЕУїРэгЩЃЎ
ЃЉЪЧЁАЙВЩњгаРэЪ§ЖдЁБТ№ЃПЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com