
 已知二次函数y=-x2+2x+3的图象与x轴交于A、B两点(A在B的左侧),与y轴交于点C,顶点为D.
已知二次函数y=-x2+2x+3的图象与x轴交于A、B两点(A在B的左侧),与y轴交于点C,顶点为D.分析 (1)先把此二次函数化为y=-(x+1)(x-3)的形式,即可求出A、B两点的坐标,由二次函数的解析式可知c=3,故可知C点坐标,由二次函数的顶点式即可求出其顶点坐标;
(2)根据四边形OCDB的面积=S矩形OEFB-S△BDF-S△CED即可解答.
解答 解:(1)∵二次函数y=-x2+2x+3可化为y=-(x+1)(x-3),A在B的左侧,
∴A(-1,0),B(3,0),
∵c=3,
∴C(0,3),
∵x=-$\frac{b}{2a}$=-$\frac{2}{2×(-1)}$=1,y=$\frac{4ac-{b}^{2}}{4a}$=$\frac{4×(-1)×3-{2}^{2}}{4×(-1)}$=4,
∴D(1,4),故此函数的大致图象为: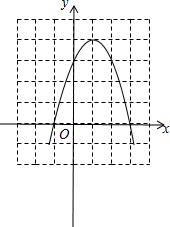
(2)连接CD、BD,
则四边形OCDB的面积=S矩形OEFB-S△BDF-S△CED
=OB•|OE|-$\frac{1}{2}$DF•|BF|-$\frac{1}{2}$DE•CE
=3×4-$\frac{1}{2}$×2×4-$\frac{1}{2}$×1×1
=12-4-$\frac{1}{2}$=$\frac{15}{2}$.
点评 本题考查的是二次函数图象的画法及矩形、三角形的面积公式,能根据题意画出图形,再利用数形结合求解是解答此题的关键.


 发散思维新课堂系列答案
发散思维新课堂系列答案科目:初中数学 来源: 题型:解答题
 如图所示,四边形OABC是矩形,点A、C的坐标分别为(6,0),(0,2),点D是线段BC上的动点(与端点B、C不重合),过点D作直线y=-x+b交折线OAB于点E.
如图所示,四边形OABC是矩形,点A、C的坐标分别为(6,0),(0,2),点D是线段BC上的动点(与端点B、C不重合),过点D作直线y=-x+b交折线OAB于点E.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 次数 | 60≤x<90 | 90≤x<120 | 120≤x<150 | 150≤x<180 | 180≤x<210 |
| 频数 | 16 | 25 | 9 | 7 | 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
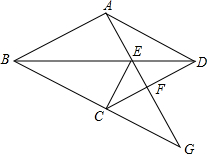 已知:如图,四边形ABCD是菱形,点G是BC延长线上一点,连接AG,分别交BD、CD于点E、F,连接CE.
已知:如图,四边形ABCD是菱形,点G是BC延长线上一点,连接AG,分别交BD、CD于点E、F,连接CE.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com