
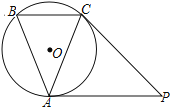
【题目】已知:AB=AC,PA=PC,若PA为△ABC的外接圆⊙O的切线
(1) 求证:PC为⊙O的切线;
(2) 连接BP,若sin∠BAC=![]() ,求tan∠BPC的值.
,求tan∠BPC的值.
【答案】(1)见解析;(2)![]()
【解析】分析:(1) 连接OA、OC, 证明△OAP≌△OCP,即可求出![]() 即可证明.
即可证明.
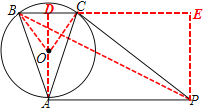
![]() 连接AO,并延长交BC于D,连接OB、OC,得到BC∥PA,根据sin∠BAC=sin∠BOD=
连接AO,并延长交BC于D,连接OB、OC,得到BC∥PA,根据sin∠BAC=sin∠BOD=![]() ,设BD=3,OB=5,则OD=4, 根据sin∠APC=sin∠PCE=
,设BD=3,OB=5,则OD=4, 根据sin∠APC=sin∠PCE=![]() ,
,
求出PC=15,CE=12, 过点C作CF⊥BP于F ,证明△BCF∽△BPE,求出![]() 的长即可求解.
的长即可求解.
详解:(1) 连接OA、OC,
∵PA为⊙O的切线,
∴∠OCP=90°,
连接OP,
可证:△OAP≌△OCP(SSS),
∴∠OAP=∠OCP=90°,
∴PC为⊙O的切线,
(2) 连接AO,并延长交BC于D,连接OB、OC,
∵AB=AC,OB=OC∴AD为线段BC的垂直平分线,
∴AD⊥BC∵AD⊥AP,
∴BC∥PA,
∵sin∠BAC=sin∠BOD=![]() ∴设BD=3,OB=5,则OD=4,
∴设BD=3,OB=5,则OD=4,
∵∠PAC=∠ACB,且AB=AC,PA=PC,
∴∠BAC=∠APC过点P作PE⊥BC交BC的延长线于E,
∴四边形APED为矩形 ,
∴PE=AD=9 ,
∴sin∠APC=sin∠PCE=![]() ,PC=15,CE=12,
,PC=15,CE=12,
过点C作CF⊥BP于F ,
∵△BCF∽△BPE
∴![]() ,CF=
,CF=![]() ,BF=
,BF=![]() ,PF=
,PF=![]() ∴tan∠BPC=
∴tan∠BPC=![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 目标测试系列答案
目标测试系列答案科目:初中数学 来源: 题型:
【题目】阅读理解
在△ABC中,AB、BC、AC三边的长分别为![]() 、
、![]() 、2,求这个三角形的面积.
、2,求这个三角形的面积.
解法一:如图1,因为△ABC是等腰三角形,并且底AC=2,根据勾股定理可以求得底边的高AF为1,所以S△ABC=![]() ×2×1=1.
×2×1=1.
解法二:建立边长为1的正方形网格,在网格中画出△ABC,使△ABC三个顶点都在小正方形的顶点处,如图2所示,借用网格面积可得S△ABC=S矩形ADEC﹣S△ABD﹣S△EBC=1.
方法迁移:请解答下面的问题:
在△ABC中,AB、AC、BC三边的长分别为![]() 、
、![]() 、
、![]() ,求这个三角形的面积.
,求这个三角形的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,AD平分∠CAB,交CB于点D,过点D作DE⊥AB,于点E
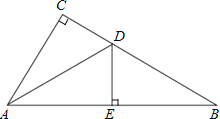
(1)求证:△ACD≌△AED;
(2)若∠B=30°,CD=1,求BD的长。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知如图,点 C 在以 AB 为直径的⊙O 上,点 D 在 AB 的延长线上,∠BCD =∠A.
(1)求证:CD 为⊙O 的切线;
(2)过点 C 作 CE⊥AB 于点 E.若 CE = 2,cos D =![]() ,求 AD 的长.
,求 AD 的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2011广西崇左,18,3分)已知:二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论中:①abc>0;②2a+b<0;③a+b<m(am+b)(m≠1的实数);④(a+c)2<b2;⑤a>1.其中正确的项是( )

A. ①⑤ B. ①②⑤ C. ②⑤ D. ①③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知x1,x2是一元二次方程(a﹣6)x2+2ax+a=0的两个实数根.
(1)是否存在实数a,使﹣x1+x1x2=4+x2成立?若存在,求出a的值;若不存在,请你说明理由;
(2)求使(x1+1)(x2+1)为正整数的实数a的整数值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)操作发现:
如图①,在![]() 中,
中,![]() ,点D是BC上一点,沿AD折叠
,点D是BC上一点,沿AD折叠![]() ,使得点C恰好落在AB上的点E处.请写出AB、AC、CD之间的关系________________________________;
,使得点C恰好落在AB上的点E处.请写出AB、AC、CD之间的关系________________________________;
(2)问题解决:
如图②,若(1)中![]() ;
;![]() ,其他条件不变,请猜想AB、AC、CD之间的关系,并证明你的结论;
,其他条件不变,请猜想AB、AC、CD之间的关系,并证明你的结论;
(3)类比探究:
如图③,在四边形ABCD中,![]() ,
,![]() ,
,![]() ,
,![]() ,连接AC、点E是CD上一点,沿AE折叠,使得点D正好落在AC上的F处,若
,连接AC、点E是CD上一点,沿AE折叠,使得点D正好落在AC上的F处,若![]() ,求DE的长.
,求DE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】恩施州绿色、富硒产品和特色农产品在国际市场上颇具竞争力,其中香菇远销日本和韩国等地.上市时,外商李经理按市场价格10元/千克在我州收购了2000千克香菇存放入冷库中.据预测,香菇的市场价格每天每千克将上涨0.5元,但冷库存放这批香菇时每天需要支出各种费用合计340元,而且香菇在冷库中最多保存110天,同时,平均每天有6千克的香菇损坏不能出售.
(1)若存放x天后,将这批香菇一次性出售,设这批香菇的销售总金额为y元,试写出y与x之间的函数关系式.
(2)李经理想获得利润22500元,需将这批香菇存放多少天后出售?(利润=销售总金额﹣收购成本﹣各种费用)
(3)李经理将这批香菇存放多少天后出售可获得最大利润?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,两个形状、大小完全相同的含有30°、60°的直角三角板如图①放置,PA、PB与直线MN重合,且三角板PAC、三角板PBD均可绕点P逆时针旋转.
(1)直接写出∠DPC的度数.
(2)如图②,在图①基础上,若三角板PAC的边PA从PN处开始绕点P逆时针旋转,转速为5°/秒,同时三角板PBD的边PB从PM处开始绕点P逆时针旋转,转速为1°/秒,(当PA转到与PM重合时,两三角板都停止转动),在旋转过程中,当PC与PB重合时,求旋转的时间是多少?
(3)在(2)的条件下,PC、PB、PD三条射线中,当其中一条射线平分另两条射线的夹角时,请直接写出旋转的时间.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com