
【题目】如图,在△ABC中,∠C=90°,将△ACE沿着AE折叠以后C点正好落在AB边上的点D处.
(1)当∠B=28°时,求∠AEC的度数;
(2)当AC=6,AB=10时,
①求线段BC的长;
②求线段DE的长.

【答案】(1) 59°;(2) ①8, ②3
【解析】
(1)在Rt△ABC中,利用互余得到∠BAC=62°,再根据折叠的性质得∠CAE=![]() ∠CAB=31°,然后根据互余可计算出∠AEC=59°;
∠CAB=31°,然后根据互余可计算出∠AEC=59°;
(2)①在Rt△ABC中,利用勾股定理即可得到BC的长;②设DE=x,则EB=BC-CE=8-x,依据勾股定理可得,Rt△BDE中DE2+BD2=BE2,再解方程即可得到DE的长.
(1)在Rt△ABC中,∠ABC=90°,∠B=28°,
∴∠BAC=90°﹣28°=62°,
∵△ACE沿着AE折叠以后C点正好落在点D处,
∴∠CAE=![]() ∠CAB=
∠CAB=![]() ×62°=31°,
×62°=31°,
Rt△ACE中,∠ACE=90°
∴∠AEC=90°﹣31°=59°.
(2)①在Rt△ABC中,AC=6,AB=10,
∴BC=![]() .
.
②∵△ACE沿着AE折叠以后C点正好落在点D处,
∴AD=AC=6,CE=DE,
∴BD=AB﹣AD=4,
设DE=x,则EB=BC﹣CE=8﹣x,
∵Rt△BDE中,DE2+BD2=BE2,
∴x2+42=(8﹣x)2,
解得x=3.
即DE的长为3.


科目:初中数学 来源: 题型:
【题目】一水果经销商购进了A,B两种水果各10箱,分配给他的甲、乙两个零售店(分别简称甲店、乙店)销售,预计每箱水果的盈利情况如下表:
A种水果/箱 | B种水果/箱 | |
甲店 | 11元 | 17元 |
乙店 | 9元 | 13元 |
(1)如果甲、乙两店各配货10箱,其中A种水果两店各5箱,B种水果两店各5箱,请你计算出经销商能盈利多少元?
(2)在甲、乙两店各配货10箱(按整箱配送),且保证乙店盈利不小于100元的条件下,请你设计出使水果经销商盈利最大的配货方案,并求出最大盈利为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将一个含有45°角的直角三角板的直角顶点放在一张宽为2cm的矩形纸带边沿上,另一个顶点在纸带的另一边沿上.若测得三角板的一边与纸带的一边所在的直线成30°角,则三角板最长边的长是( )

A. 2cm B. 4cm C. 2![]() cm D. 4
cm D. 4![]() cm
cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,圆柱形玻璃杯高为12cm、底面周长为18cm,在杯内离杯底4cm的点C
处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿4cm与蜂蜜相对的点A处,则蚂蚁到达蜂蜜的最
短距离为 ▲ cm.

查看答案和解析>>
科目:初中数学 来源: 题型:
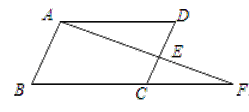
【题目】如图,根据图形填空:
已知:∠DAF=∠F,∠B=∠D,AB与DC平行吗?
解:∠DAF=∠F ( )
∴AD∥BF( ),
∴∠D=∠DCF( )
∵∠B=∠D ( )
∴∠B=∠DCF ( )
∴AB∥DC( )
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线Y=ax2+bx一3与X轴相交于A(一1,0),B(3,0),P为抛物线上第四象限上的点.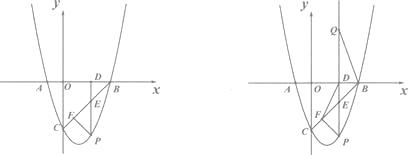
(1)求该抛物线的函数关系式.
(2)过点P作PD⊥X轴于点D,PD交BC于点E,当线段PE的长度最大时,求点P的坐标.
(3)当线段PE的长度最大时,作PF ⊥BC于点F,连结DF.在射线PD上有一点Q,满足∠PQB=∠DFB,问在坐标轴上是否存在一点R,使得S△RBE=S△QBE;如果存在,直接写出R点的坐标;如果不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】以下是两张不同类型火车的车票:(“D×××次”表示动车,“G×××次”表示高铁):
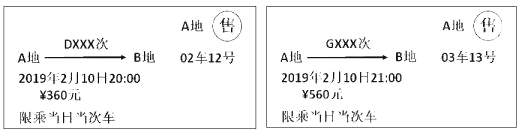
(1)根据车票中的信息填空:两车行驶方向 ,出发时刻 (填“相同”或“不同”);
(2)已知该动车和高铁的平均速度分别为200km/h,300km/h,如果两车均按车票信息准时出发,且同时到达终点,求A,B两地之间的距离;
(3)在(2)的条件下,请求出在什么时刻两车相距100km?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在ABCD中,∠BAD的平分线交直线BC于点E,交直线DC于点F.
(1)在图1中证明CE=CF;
(2)若∠ABC=90°,G是EF的中点(如图2),直接写出∠BDG的度数;
(3)若∠ABC=120°,FG∥CE,FG=CE,分别连接DB、DG(如图3),求∠BDG的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com