
【题目】如图,四边形ABCD是菱形,∠A=60°,AB=2,扇形BEF的半径为2,圆心角为60°,则图中阴影部分的面积是( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
科目:初中数学 来源: 题型:
【题目】如图1,若△ABC和△ADE为等边三角形,M,N分别是BE,CD的中点,
(1)求证:△AMN是等边三角形.
(2)当把△ADE绕A点旋转到图2的位置时,CD=BE是否仍然成立?若成立请证明,若不成立请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠1+∠2=180°,∠A=∠C,DA平分∠BDF.
(1)AE与FC会平行吗?说明理由;
(2)AD与BC的位置关系如何?为什么?
(3)BC平分∠DBE吗?为什么.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O是△ABC的外接圆,AD是⊙O的直径,AD与BC相交于点M,且BM=MC,过点D作BC的平行线,分别与AB、AC的延长线相交于点E、F.
(1)求证:EF与⊙O相切;
(2)若BC=2![]() ,MD=
,MD=![]() ,求CE的长.
,求CE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】受气候的影响,某超市蔬菜供应紧张,需每天从外地调运蔬菜1000斤.超市决定从甲、乙两大型蔬菜棚调运蔬菜,已知甲蔬菜棚每天最多可调出800斤,乙蔬菜棚每天最多可调运600斤,从两蔬菜棚调运蔬菜到超市的路程和运费如下表:
到超市的路程(千米) | 运费(元/斤·千米) | |
甲蔬菜棚 | 120 | 0.03 |
乙蔬菜棚 | 80 | 0.05 |
(1)若某天调运蔬菜的总运费为3840元,则从甲、乙两蔬菜棚各调运了多少斤蔬菜?
(2)设从甲蔬菜棚调运蔬菜![]() 斤,总运费为
斤,总运费为![]() 元,试写出
元,试写出![]() 与
与![]() 的函数关系式,怎样安排调运方案才能使每天的总运费最省?
的函数关系式,怎样安排调运方案才能使每天的总运费最省?
查看答案和解析>>
科目:初中数学 来源: 题型:
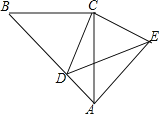
【题目】如图,△ACB与△CED都是等腰直角三角形,∠BCA=∠DCE=90°,且点D在线段AB上,连接AE.
(1)求证:①△BCD≌△ACE;②∠DAE=90°;
(2)若AB=8,当点D在线段AB上什么位置时,四边形ADCE的周长最小?请说明并求出周长的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
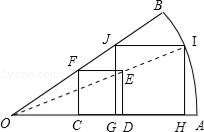
【题目】小明手上一张扇形纸片OAB.现要求在纸片上截一个正方形,使它的面积尽可能大.
小明的方案是:如图,在扇形纸片OAB内,画正方形CDEF,使C、D在OA上,F在OB上;连接OE并延长交弧AB于I,画IH∥ED交OA于H,IJ∥OA交OB于J,再画JG∥FC交OA于G.
(1)你认为小明画出的四边形GHIJ是正方形吗?如果是,请证明.如果不是,请说明理由.
(2)如果扇形OAB的圆心角∠AOB=30°,OA=6cm,小明截得的四边形GHIJ面积是多少(结果精确到0.1cm).
(3)(1)中小明画出的四边形GHIJ如果是正方形,我们把它叫做扇形的内接正方形(四个顶点分别在扇形的半径和弧上).请你再画出一种不同于图(1)的扇形的内接正方形(保留画图痕迹,不要求证明)
查看答案和解析>>
科目:初中数学 来源: 题型:
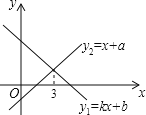
【题目】一次函数![]() 与
与![]() 的图象如图,则下列结论①
的图象如图,则下列结论①![]() ②
②![]() ,且
,且![]() 的值随着
的值随着![]() 值的增大而减小.③关于
值的增大而减小.③关于![]() 的方程
的方程![]() 的解是
的解是![]() ④当
④当![]() 时,
时,![]() ,其中正确的有___________.(只填写序号)
,其中正确的有___________.(只填写序号)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com