练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

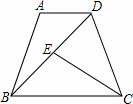
    已知：如图，在等腰梯形ABCD中，AD∥BC，∠BDC=∠BCD，点E是线段BD上一点，且BE=AD．

    （1）证明：△ADB≌△EBC；

    （2）直接写出图中所有的等腰三角形．


    解答：

    解（1）∵AD∥BC，

    ∴∠ADB=∠EBC，

    ∵∠BDC=∠BCD，

    ∴BD=BC，

    在△ADB和△EBC中，

    ∴△ADB≌△EBC（SAS）．（2）由（1）可得△BCD是等腰三角形；

    ∵△ADB≌△EBC，

    ∴CE=AB，

    又∵AB=CD，

    ∴CE=CD，

    ∴△CDE是等腰三角形．


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：


     下列的几何图形中，一定是轴对称图形的有

     


    A.  5个              B.  4个            C.  3个             D.  2个

    查看答案和解析>>

    科目：初中数学 来源： 题型：


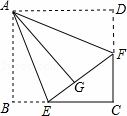
    如图，点E、F分别是正方形纸片ABCD的边BC、CD上一点，将正方形纸片ABCD分别沿AE、AF折叠，使得点B、D恰好都落在点G处，且EG=2，FG=3，则正方形纸片ABCD的边长为　　．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    下列计算正确的是（　　）

    　

    A．

    B．

    （x+y）2=x2+y2

    C．

    （﹣3x）3=﹣9x3

    D．

    ﹣（x﹣6）=6﹣x

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    一个圆锥的母线长为4，侧面积为8π，则这个圆锥的底面圆的半径是　

    查看答案和解析>>

    科目：初中数学 来源： 题型：


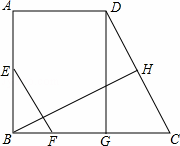
    如图，在梯形ABCD中，AD∥BC，∠ABC=90°，DG⊥BC于G，BH⊥DC于H，CH=DH，点E在AB上，点F在BC上，并且EF∥DC．

    （1）若AD=3，CG=2，求CD；

    （2）若CF=AD+BF，求证：EF=CD．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，△ABC中，已知AB=8，∠C=90°，∠A=30°，DE是中位线，则DE的长为（　　）

    　

    A．

    4

    B．

    3

    C．

    D．

    2

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    已知P（﹣3，m）和Q（1，m）是抛物线y=2x2+bx+1上的两点．

    （1）求b的值；

    （2）判断关于x的一元二次方程2x2+bx+1=0是否有实数根，若有，求出它的实数根；若没有，请说明理由；

    （3）将抛物线y=2x2+bx+1的图象向上平移k（k是正整数）个单位，使平移后的图象与x轴无交点，求k的最小值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    以为解的一个二元一次方程是_________．

    查看答案和解析>>

    同步练习册答案