解:(1)原式=1+7+3=11;
(2)原式=-9×

×(-

)+8
=1+8
=9;
(3)原式=2a
2b-4ab
2+2c-2c-3a
2b+ab
2,
=-a
2b-3ab
2.
(4)原式=-8+6+3-1=0;
(5)原式=3x
2y-6xy+8xy-4+x
2y+1=4x
2y+2xy-3,
当x=-

时,原式=4x
2y+2xy-3=-3.
(6)(2mx
2+5x
2+3x+1)-(5x
2-4y
2+3x)化简得2mx
2+4y
2+1
∵化简后不含x
2项.
∴2m=0即m=0,
∴2m
3-[3m
3-(4m-5)+m]=-5.
(7)①移项合并得:x=4;
②去分母得:4(x+1)=5(x+1)-6,
移项合并得:(x+1)=6,
∴可得:x=5.
分析:(1)直接进行有理数的加减运算即可.
(2)先进行幂的运算,然后再根据先乘除后加减的法则进行计算.
(3)先去括号,然后合并同类项即可得出答案.
(4)先进行幂和绝对值的运算,然后再根据先乘除后加减的法则进行计算.
(5)先去括号,然后合并同类项得出最简整式,然后再将x的值代入即可.
(6)化简后不含x
2项即可得出x
2项的系数为0,从而可得m的值,将要求整式化为最简后代入m的值可得出答案.
(7)①移项合并后即可得出答案;②将(x+1)看作一个整体,先去分母,然后移项合并,最后化系数为1,求出x+1的值后即可得出x的值.
点评:本题考查了整式的化简求值及解方程的知识,有一应难度,综合性比较强,注意在运算时要细心.

 )-(-2)3
)-(-2)3
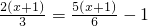 .
. ×(-
×(- )+8
)+8 时,原式=4x2y+2xy-3=-3.
时,原式=4x2y+2xy-3=-3.

 同步拓展阅读系列答案
同步拓展阅读系列答案