
【题目】学完第2章“特殊的三角形”后,老师布置了一道思考题:
如图,点M、N分别在正三角形ABC的BC,CA边上,且BM=CN,AM,BN交于点Q.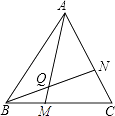
(1)判断△ABM与△BCN是否全等,并说明理由.
(2)判断∠BQM是否会等于60°,并说明理由.
(3)若将题中的点M,N分别移动到BC,CA的延长线上,且BM=CN,是否能得到∠BQM=60°?请说明理由. 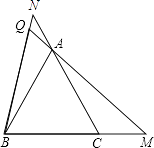
【答案】
(1)解:全等,理由:
∵AB=BC,∠ABM=∠BCN=60°,BM=CN,
∴△ABM≌△BCN(SAS);
(2)解:∵△ABM≌△BCN,
∴∠CBN=∠BAM,
∴∠BQM=∠BAM+∠ABQ=∠CBN+∠ABQ=∠ABC=60°;
(3)解:能得到∠BQM=60°.理由如下:
同(1)可证△ABM≌△BCN(SAS),
∴∠M=∠N,
∵∠QAN=∠CAM,∠BQM=∠N+∠QAN,∠ACB=∠M+∠CAM,
∴∠BQM=∠ACB=60°.
【解析】(1)因为AB=BC,∠ABM=∠BCN=60°,BM=CN,利用SAS可以证明;(2)根据两个三角形全等,对应角相等可得∠CBN=∠BAM,则∠BQM=∠BAM+∠ABQ=∠CBN+∠ABQ=∠ABC=60°;(3)和(1)同样的求法可得△ABM≌△BCN,然后利用三角形外角的性质求∠BQM=60°.
【考点精析】解答此题的关键在于理解等边三角形的性质的相关知识,掌握等边三角形的三个角都相等并且每个角都是60°.


科目:初中数学 来源: 题型:
【题目】将一副三角尺如图拼接:含30°角的三角尺(△ABC)的长直角边与含45°角的三角尺(△ACD)的斜边恰好重合.已知AB=2 ![]() ,P是AC上的一个动点.
,P是AC上的一个动点.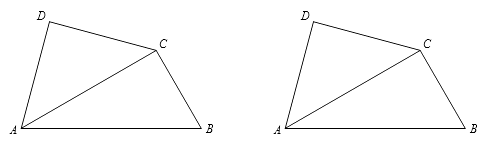
(1)当点P运动到∠ABC的平分线上时,连接DP、BP,求CP、DP的长;
(2)当点P在运动过程中出现PD=BC时,求此时∠PDA的度数;
(3)当点P运动到什么位置时,以D,P,B,Q为顶点的平行四边形的顶点Q恰好在边BC上?求出此时平行四边形的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一般情况下,学生注意力上课后逐渐增强,中间有段时间处于较理想的稳定状态,随后开始分散.实验结果表明,学生注意力指数y随时间x(min)的变化规律如图所示(其中AB、BC分别为线段,CD为双曲线的一部分):
(1)上课后第5min与第30min相比较,何时学生注意力更集中?
(2)某道难题需连续讲19min,为保证效果,学生注意力指数不宜低于36,老师能否在所需要求下讲完这道题?
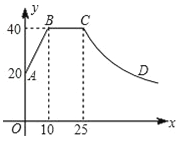
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知整数 a1 , a2 , a3 , a4 , …满足下列条件:a1=0,a2=﹣|a1+1|,a3=﹣|a2+2|,a4=﹣|a3+3|,…,依此类推,则a2017的值为( )
A.﹣1005
B.﹣1006
C.﹣1007
D.﹣1008
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在创建“全国文明城市”和“省级文明城区”过程中,栾城区污水处理厂决定先购买A、B两型污水处理设备共20台,对城区周边污水进行处理.已知每台A型设备价格为12万元,每台B型设备价格为10万元;1台A型设备和2台B型设备每周可以处理污水640吨,2台A型设备和3台B型设备每周可以处理污水1080吨.
(1)求A、B两型污水处理设备每周分别可以处理污水多少吨?
(2)要想使污水处理厂购买设备的资金不超过230万元,但每周处理污水的量又不低于4500吨,请你列举出所有购买方案,并指出哪种方案所需资金最少?最少是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com