
【题目】为创建足球特色学校,营造足球文化氛围,某学校随机抽取部分八年级学生足球运球的测试成绩作为一个样本,按A,B,C,D四个等级进行统计,制成了如下不完整的统计图.(说明:A级:8分—10分,B级:7分—7.9分,C级:6分—6.9分,D级:1分—5.9分)根据所给信息,解答以下问题:
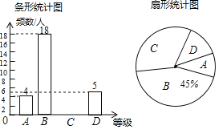
(1)样本容量为 ,C对应的扇形的圆心角是____度,补全条形统计图;
(2)所抽取学生的足球运球测试成绩的中位数会落在____等级;
(3)该校八年级有300名学生,请估计足球运球测试成绩达到![]() 级的学生有多少人?
级的学生有多少人?
【答案】(1)40人,117;(2)B;(3)30人.
【解析】
(1)根据B等级的学生数和所占的百分比可以求得本次调查的学生数;求出C的人数,再计算出所占比例即可求出对应的扇形的圆心角的度数;从而可以将条形统计图补充完整;
(2)根据统计图中的数据可以得到所抽取学生的足球运球测试成绩的中位数落在哪个等级;
(3)根据统计图中的数据可以求得足球运球测试成绩达到A级的学生有多少人.
(1)18÷45%=40,
即在这次调查中一共抽取了40名学生,
C等级的人数为:40-4-18-5=13,
在扇形统计图中,C对应的扇形的圆心角是:360°×![]() =117°,
=117°,
补全的条形统计图如图所示:
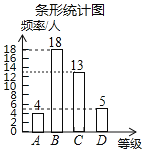
(2)由统计图可知,
所抽取学生的足球运球测试成绩的中位数落在B等级,
故答案为:B;
(5)300×![]() =30(人),
=30(人),
答:足球运球测试成绩达到A级的学生有30人.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】下面说法中正确的个数有( )
①等腰三角形的高与中线重合
②一组对边平行,另一组对边相等的四边形是平行四边形
③顺次连接任意四边形的中点组成的新四边形为平行四边形
④七边形的内角和为900°,外角和为360°
⑤如果方程![]() 会产生增根,那么k的值是4
会产生增根,那么k的值是4
A. 1个B. 2个C. 3个D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
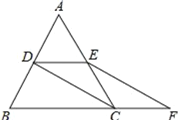
【题目】如图,等边△ABC的边长是2,D、E分别为AB、AC的中点,过点E作EF∥CD交BC的延长线于点F,连接CD.
(1)求证:DE=CF;
(2)求EF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
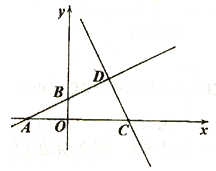
【题目】如图,已知A(-4,0)、B(0,2)、C(6,0),直线AB与直线CD相交于点D,D点的横纵坐标相同;
(1)求点D的坐标;
(2)点P从O出发,以每秒1个单位的速度沿x轴正半轴匀速运动,过点P作x轴的垂线分别与直线AB、CD交于E、F两点,设点P的运动时间为t秒,线段EF的长为y(y>0),求y与t之间的函数关系式,并直接写出自变量t的取值范围;
(3)在(2)的条件下,直线CD上是否存在点Q,使得△BPQ是以P为直角顶点的等腰直角三角形?若存在,请求出符合条件的Q点坐标,若不存在,请说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
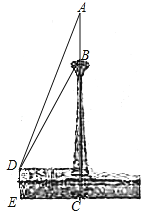
【题目】如图所示,天津电视塔顶部有一桅杆部分AB,数学兴趣小组的同学在距地面高为4.2m的平台D处观测电视塔桅杆顶部A的仰角为67.3°,观测桅杆底部B的仰角为58°.已知点A,B,C在同一条直线上,EC=172m.求测得的桅杆部分AB的高度和电视塔AC的高度.(结果保留小数点后一位).
参考数据:tan67.3°≈2.39,tan60°≈1.73.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某天上午,一出租车司机始终在一条南北走向的笔直马路上营运,(出发点记作为点O,约定向南为正,向北为负),期间一共运载6名乘客,行车里程(单位:千米)依先后次序记录如下:﹢7,﹣3,﹢6,﹣1,﹢2,﹣4.
(1)出租车在行驶过程中,离出发点O最远的距离是______千米;
(2)将最后一名乘客送到目的地,出租车离出发点O多远?在O点的什么方向?
(3)出租车收费标准为:起步价(不超过3千米)为8元,超过3千米的部分每千米的价格为1.5元,求司机这天上午的营业额.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某体院要了解篮球专业学生投篮的命中率,对学生进行定点投篮测试,规定每人投篮20次,测试结束后随机抽查了一部分学生投中的次数,并分为五类,Ⅰ:投中11次;Ⅱ投中12次;Ⅲ:投中13次;Ⅳ:投中14次;Ⅴ:投中15次.根据调查结果绘制了下面尚不完整的统计图1、图2: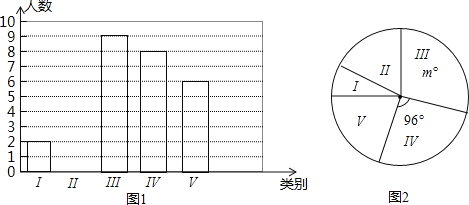
回答下列问题:
(1)本次抽查了 名学生,图2中的m= .
(2)补全条形统计图,并指出中位数在哪一类.
(3)求最高的命中率及命中最高的人数所占的百分比.
(4)若体院规定篮球专业学生定点投篮命中率不低于65%记作合格,估计该院篮球专业210名学生中约有多少人不合格.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司从2014年开始投入技术改进资金,经技术改进后,其产品的成本不断降低,具体数据如下表:
年 度 | 2013 | 2014 | 2015 | 2016 |
投入技改资金 | 2.5 | 3 | 4 | 4.5 |
产品成本 | 7.2 | 6 | 4.5 | 4 |
(1)请你认真分析表中数据,从一次函数和反比例函数中确定哪一个函数能表示其变化规律,给出理由,并求出其解析式;
(2)按照这种变化规律,若2017年已投入资金5万元.
①预计生产成本每件比2016年降低多少万元?
②若打算在2017年把每件产品成本降低到3.2万元,则还需要投入技改资金多少万元?(结果精确到0.01万元).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是按照一定规律画出的“树形图”,经观察可以发现:图A2比图A1多出2个“树枝”,图A3比图A2多出4个“树枝”,图A4比图A3多出8个“树枝”……照此规律,图A6比图A2多出“树枝”( )
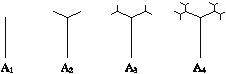
A.32个B.56个C.60个D.64个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com