
| A. | 矩形 | B. | 菱形 | C. | 正方形 | D. | 无法确定 |
科目:初中数学 来源: 题型:解答题
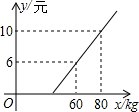 某地长途汽车客运公司规定旅客可随身携带一定重量的行李,如果超过规定重量,则需要买行李票,已知行李票费y(元)是其重量x(千克)的一次函数,(如图所示):
某地长途汽车客运公司规定旅客可随身携带一定重量的行李,如果超过规定重量,则需要买行李票,已知行李票费y(元)是其重量x(千克)的一次函数,(如图所示):查看答案和解析>>
科目:初中数学 来源: 题型:解答题
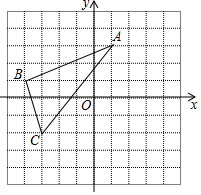 如图,△ABC在平面直角坐标系中,且A(1,3)、B(-4,1)、C(-3,-2).
如图,△ABC在平面直角坐标系中,且A(1,3)、B(-4,1)、C(-3,-2).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
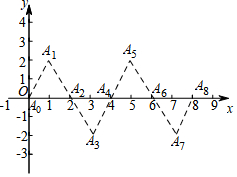 如图所示点A0(0,0),A1(1,2),A2(2,0),A3(3,-2),A4(4,0),…根据这个规律,探究可得点A2017坐标是(2017,2).
如图所示点A0(0,0),A1(1,2),A2(2,0),A3(3,-2),A4(4,0),…根据这个规律,探究可得点A2017坐标是(2017,2).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 电器类型 | 进价(元)/台 | 售价(元)/台 |
| 甲 | 1500 | 1900 |
| 乙 | 1800 | 2400 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com