
【题目】(8分)【问题情境】
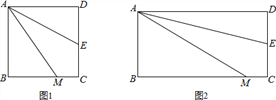
如图1,四边形ABCD是正方形,M是BC边上的一点,E是CD边的中点,AE平分∠DAM.
【探究展示】(1)证明:AM=AD+MC;
【拓展延伸】(2)若四边形ABCD是长与宽不相等的矩形,其他条件不变,如图2,探究展示(1)中的结论是否成立?请作出判断,不需要证明.
【答案】(1)见解析;(2)仍然成立.
【解析】整体分析:
(1)延长AE、BC交于点N,由△ADE≌△NCE,证AD=NC,由角平分线,平行线得MA=MN;(2)与(1)的方法类似.
(1)证明:延长AE、BC交于点N,如图1,
∵四边形ABCD是正方形,∴AD∥BC.∴∠DAE=∠ENC.∵AE平分∠DAM,∴∠DAE=∠MAE.
∴∠ENC=∠MAE.∴MA=MN.
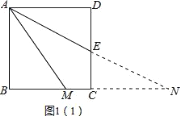
∴△ADE≌△NCE(AAS)
∴AD=NC.∴MA=MN=NC+MC=AD+MC.
(2)①结论AM=AD+MC仍然成立.
证明:延长AE、BC交于点P,如图2,
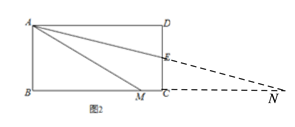
∵四边形ABCD是矩形,∴AD∥BC.∴∠DAE=∠EPC.
∵AE平分∠DAM,∴∠DAE=∠MAE.
∴∠EPC=∠MAE.∴MA=MP.
∴△ADE≌△PCE(AAS).
∴AD=PC.∴MA=MP=PC+MC=AD+MC.


科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=﹣x2+mx+3与x轴交于A,B两点,与y轴交于点C,点B的坐标为(3,0) 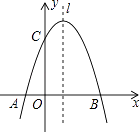
(1)求m的值及抛物线的顶点坐标.
(2)点P是抛物线对称轴l上的一个动点,当PA+PC的值最小时,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
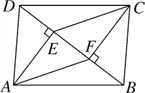
【题目】四边形ABCD中,AD=BC,BE=DF,AE⊥BD,CF⊥BD,垂足分别为点E,F.
(1)求证:△ADE≌△CBF;
(2)若AC与BD相交于点O,求证:AO=CO.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】先阅读下列解题过程,再解答问题:
-5![]() +7
+7![]() =-5+(-
=-5+(-![]() )+7+
)+7+![]() =[(-5)+7]+[(-
=[(-5)+7]+[(-![]() )+
)+![]() ]=2+
]=2+![]() =2
=2![]() .
.
上述方法叫做拆项法,依照上述方法计算:
(1)7![]() +(-7
+(-7![]() );
);
(2)(-2018![]() )+(-2017
)+(-2017![]() )+4036
)+4036![]() +(-1
+(-1![]() ).
).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=4cm,AD=12cm,点P在AD边上以每秒1cm的速度从点A向点D运动,点Q在BC边上,以每秒4cm的速度从点C出发,在CB间往返运动,两个点同时出发,当点P到达点D时停止(同时点Q也停止),在这段时间内,线段PQ有( )次平行于AB?

A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点C是线段AB上一点,M是线段AC的中点,N是线段BC的中点.
(1)如果AB=10cm,AM=3cm,求CN的长;
(2)如果MN=6cm,求AB的长.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角坐标平面中,O为原点,点A的坐标为(20,0),点B在第一象限内,BO=10,sin∠BOA= ![]() .
. 
(1)在图中,求作△ABO的外接圆(尺规作图,不写作法但需保留作图痕迹);
(2)求点B的坐标与cos∠BAO的值;
(3)若A,O位置不变,将点B沿x轴向右平移使得△ABO为等腰三角形,请求出平移后点B的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
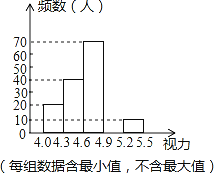
【题目】某校为了解八年级学生的视力情况,对八年级的学生进行了一次视力调查,并将调查数据进行统计整理,绘制出如下频数分布表和频数分布直方图的一部分.
视力 | 频数(人) | 频率 |
4.0≤x<4.3 | 20 | 0.1 |
4.3≤x<4.6 | 40 | 0.2 |
4.6≤x<4.9 | 70 | 0.35 |
4.9≤x<5.2 | a | 0.3 |
5.2≤x<5.5 | 10 | b |
(1)在频数分布表中,a= ,b= ;
(2)将频数分布直方图补充完整;
(3)若视力在4.6以上(含4.6)均属正常,求视力正常的人数占被调查人数的百分比是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司招聘职员,对甲、乙两位候选人进行了面试和笔试,面试中包括形体和口才,笔试中包括专业水平和创新能力考察,他们的成绩(百分制)如下表:
候选人 | 面试 | 笔试 | ||
形体 | 口才 | 专业水平 | 创新能力 | |
甲 | 86 | 90 | 96 | 92 |
乙 | 92 | 88 | 95 | 93 |
若公司根据经营性质和岗位要求认为:形体、口才、专业水平、创新能力按照5:5:4:6的比确定,请计算甲、乙两人各自的平均成绩,看看谁将被录取?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com