
【题目】一个不透明的口袋里装有红、黄、绿三种颜色的球(除颜色不同外其余都相同),其中红球有2个,黄球有1个,从中任意捧出1球是红球的概率为![]() .
.
(1)试求袋中绿球的个数;
(2)第1次从袋中任意摸出1球(不放回),第2次再任意摸出1球,请你用画树状图或列表格的方法,求两次都摸到红球的概率.

【答案】(1)绿球有1个(2)![]()
【解析】试题分析:(1)此题的求解方法是:借助于方程求解;(2)根据简单事件的概率求法解答即可;(3)此题需要两步完成,所以采用树状图或者列表法都比较简单.
试题解析::(1)设绿球的个数为x.由题意,得: ![]() ,解得x=1,经检验x=1是所列方程的根,所以绿球有1个;(2)P(任意摸出一个球是黄球)=
,解得x=1,经检验x=1是所列方程的根,所以绿球有1个;(2)P(任意摸出一个球是黄球)=![]() ,(3)根据题意,画树状图:
,(3)根据题意,画树状图:
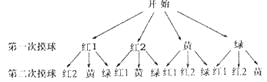
由图知共有12种等可能的结果,即(红1,红2),(红1,黄),(红1,绿),(红2,红1),(红2,黄),(红2,绿),(黄,红1),(黄,红2),(黄,绿),(绿,红1),(绿,红2),(绿,黄),其中两次都摸到红球的结果有两种(红,红),(红,红).∴P(两次都摸到红球)=![]() ;
;
或根据题意,画表格:
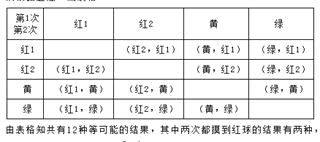
∴P(两次都摸到红球)=![]() .
.


科目:初中数学 来源: 题型:
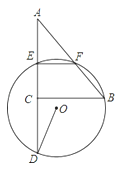
【题目】如图,△ABC中,AC=3,BC=4,∠ACB=90°,E、F分别为AC、AB的中点,过E、F两点作⊙O,延长AC交⊙O于D.若∠CDO=![]() ∠B,则⊙O的半径为( )
∠B,则⊙O的半径为( )
A. 4 B. 2![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
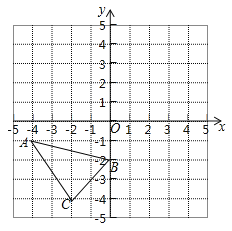
【题目】如图,△ABC的三个顶点都在边长为1的小正方形组成的网格的格点上,以点O为原点建立直角坐标系,回答下列问题:
(1)将△ABC先向上平移5个单位,再向右平移1个单位得到△A1B1C1,画出△A1B1C1,并直接写出A1的坐标 ;
(2)将△A1B1C1绕点(0,﹣1)顺时针旋转90°得到△A2B2C2,画出A2B2C2;
(3)观察图形发现,A2B2C2是由△ABC绕点 顺时针旋转 度得到的.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,是一块在电脑屏幕上出现的长方形色块图,由6个不同的正方形组成。设中间最小的一个正方形边长为1,则这个长方形色块图的面积为_____________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】A,B两种型号的空调,已知购进3台A型号空调和5台B型号空调共用14500元;购进4台A型号空调和10台B型号空调共用25000元.
(1)求A,B两种型号空调的进价;
(2)若超市准备用不超过54000元的资金再购进这两种型号的空调共30台,求最多能购进A种型号的空调多少台?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=kx+b的图象与反比例函数y=![]() 的图象交于A(﹣2,1),B(1,n)两点.
的图象交于A(﹣2,1),B(1,n)两点.
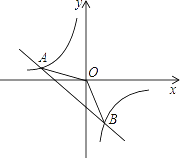
(1)试确定上述反比例函数和一次函数的表达式;
(2)求△AOB的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线![]() 分别与
分别与![]() 轴、
轴、![]() 轴交于
轴交于![]() 、
、![]() 两点,与直线
两点,与直线![]() 交于点
交于点![]() ,平行于
,平行于![]() 轴的直线
轴的直线![]() 从原点
从原点![]() 出发,以每秒1个单位长度的速度沿
出发,以每秒1个单位长度的速度沿![]() 轴向右平移,直线
轴向右平移,直线![]() 分别交直线
分别交直线![]() 、直线
、直线![]() 于点
于点![]() 、
、![]() ,以
,以![]() 为边向左侧作正方形
为边向左侧作正方形![]() ,当直线
,当直线![]() 经过点
经过点![]() 时停止运动,设直线
时停止运动,设直线![]() 的运动时间为
的运动时间为![]() (秒).
(秒).
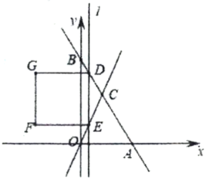
(1)![]() ________,
________,![]() ________;
________;
(2)设线段![]() 的长度为
的长度为![]() (
(![]() );求
);求![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(3)当正方形![]() 的边
的边![]() 落在
落在![]() 轴上时,求出
轴上时,求出![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知等边三角形ABC的边长是2,以BC边上的高AB1为边作等边三角形,得到第一个等边三角形AB1C1,再以等边三角形AB1C1的B1C1边上的高AB2为边作等边三角形,得到第二个等边三角形AB2C2,再以等边三角形AB2C2的边B2C2边上的高AB3为边作等边三角形,得到第三个等边AB3C3;…,如此下去,这样得到的第n个等边三角形ABnCn的面积为 .

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com