
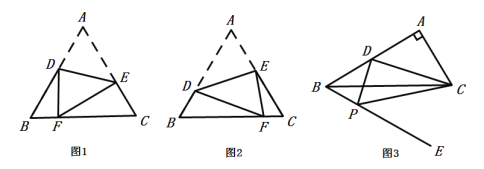
【题目】(1)如图1,△ABC为等边三角形,点D、E分别为边AB、AC上的一点,将图形沿线段DE所在的直线翻折,使点A落在BC边上的点F处求证:![]() ;
;
(2)如图2,按图1的翻折方式,若等边△ABC的边长为4,当![]() 时,求
时,求![]() 的值;
的值;
(3)如图3,在![]() 中,
中,![]() ,点D是AB边上的中点,在BC的下方作射线BE,使得
,点D是AB边上的中点,在BC的下方作射线BE,使得![]() ,点P是射线BE上一个动点,当
,点P是射线BE上一个动点,当![]() ,求BP的长.
,求BP的长.
【答案】(1)见解析;(2)![]() ;(3)2或6
;(3)2或6
【解析】
(1)根据三角形外角的性质证明∠BDF=∠EFC,从而可得△BDF∽△CFE,根据相似三角形对应边成比例即可得出结论;
(2)过D作DH⊥BC.设BF=x,则CF=4-x.设EF=2a,则DF=3a,AE=2a,BD=4-AD=4-3a,CE=4-AE=4-2a,由相似三角形对应边成比例,即可得出x、a的值,从而求得BD、DF、DH的长,根据正弦的定义即可得出结论;
(3)解Rt△ABC得到BC、AB、BD的长.过C作CF⊥BC,交BE于F,解Rt△BCF,得到CF、BF的长.通过证明△DBPΔPFC,由相似三角形对应边成比例即可得出结论.
(1)![]() ,
,
又![]() ,
,
![]() ,
,
![]() .
.
又![]() ,
,
![]() ,
,
![]() ,
,
即![]() .
.
(2)过D作![]() .
.

设![]() ,则
,则![]() .
.
设![]() ,则
,则![]() ,AE=2a,
,AE=2a,
![]() ,
,
![]() .
.
由(1)知![]() ,
,
![]() ,
,
即![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
![]() ,
,
![]() ,
,
![]() .
.
(3)∵![]() ,
,
∴![]() ,
,
![]() ,
,
∴![]() .
.
过C作![]() ,交BE于F.
,交BE于F.
∵∠CBF=30°,
∴![]() CF=BC=
CF=BC=![]() ,
,
∴CF=4,∴BF=2CF=8.
∵![]()
![]() ,
,
![]() .
.
∴![]() ,
,
又![]() ,
,
∴![]() ,
,
∴![]() ,即
,即![]() ,
,
∴![]() 或6.
或6.



 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案科目:初中数学 来源: 题型:
【题目】阅读下面内容,并按要求解决问题: 问题:“在平面内,已知分别有![]() 个点,
个点,![]() 个点,
个点,![]() 个点,5 个点,…,n 个点,其中任意三 个点都不在同一条直线上.经过每两点画一条直线,它们可以分别画多少条直线? ” 探究:为了解决这个问题,希望小组的同学们设计了如下表格进行探究:(为了方便研 究问题,图中每条线段表示过线段两端点的一条直线)
个点,5 个点,…,n 个点,其中任意三 个点都不在同一条直线上.经过每两点画一条直线,它们可以分别画多少条直线? ” 探究:为了解决这个问题,希望小组的同学们设计了如下表格进行探究:(为了方便研 究问题,图中每条线段表示过线段两端点的一条直线)

请解答下列问题:
(1)请帮助希望小组归纳,并直接写出结论:当平面内有![]() 个点时,直线条数为 ;
个点时,直线条数为 ;
(2)若某同学按照本题中的方法,共画了![]() 条直线,求该平面内有多少个已知点.
条直线,求该平面内有多少个已知点.
查看答案和解析>>
科目:初中数学 来源: 题型:
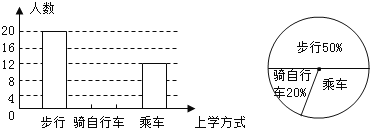
【题目】学习了统计知识后,小明的数学老师要求每个学生就本班同学的上学方式进行一次调查统计,如图是小明通过收集数据后绘制的两幅不完整的统计图. 请根据图中提供的信息,解答下列问题:
(1)该班共有_______________名学生;
(2)将“骑自行车”部分的条形统计图补充完整;
(3)在扇形统计图中;求出“乘车”部分所对应的圆心角的度数;
(4)若全年级有600名学生,试估计该年级骑自行车上学的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程![]() 有两个实数根x1,x2.
有两个实数根x1,x2.
(1)求实数k的取值范围;
(2)是否存在实数k使得![]() 成立?若存在,请求出k的值;若不存在,请说明理由.
成立?若存在,请求出k的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店经过市场调查,整理出某种商品在第![]() (
(![]() )天的售价与销量的相关信息如下表.已知该商品的进价为每件30元,设销售该商品每天的利润为
)天的售价与销量的相关信息如下表.已知该商品的进价为每件30元,设销售该商品每天的利润为![]() 元.
元.
(1)求![]() 与
与![]() 的函数关系是;
的函数关系是;
(2)问销售该商品第几天时,当天销售利润最大,最大利润是多少?
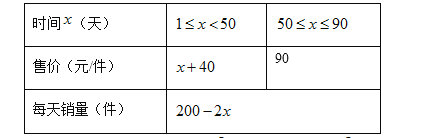
查看答案和解析>>
科目:初中数学 来源: 题型:
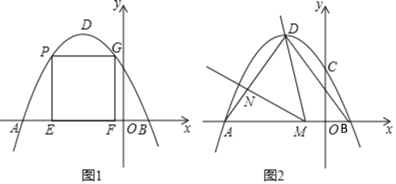
【题目】如图1,在平面直角坐标系中,抛物线y=﹣![]() x2+bx+c经过点A(﹣5,0)和点B(1,0).
x2+bx+c经过点A(﹣5,0)和点B(1,0).
(1)求抛物线的解析式及顶点D的坐标;
(2)点P是抛物线上A、D之间的一点,过点P作PE⊥x轴于点E,PG⊥y轴,交抛物线于点G,过点G作GF⊥x轴于点F,当矩形PEFG的周长最大时,求点P的横坐标;
(3)如图2,连接AD、BD,点M在线段AB上(不与A、B重合),作∠DMN=∠DBA,MN交线段AD于点N,是否存在这样点M,使得△DMN为等腰三角形?若存在,求出AN的长;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com