
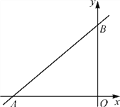
【题目】如图,直线y=kx+6与x轴,y轴分别相交于点A,B,O为坐标原点,点A的坐标为(-8,0).
(1)求k的值;
(2)若点P(x,y)是第二象限内直线上的一个动点,在点P的运动过程中,试写出△OPA的面积S与x之间的函数关系式,并写出自变量的取值范围;
(3)若点P(0,m)为射线BO(B,O两点除外)上的一动点,过点P作PC⊥y轴交直线AB于C,连接PA.设△PAC的面积为S′,求S′与m的函数关系式,并写出自变量m的取值范围.
【答案】(1)![]() (2)S=3x+24(-8<x<0)(3) S′=
(2)S=3x+24(-8<x<0)(3) S′=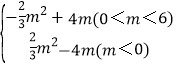
【解析】(1)将点A的坐标代入直线y=kx+6中,即可求得k的值.
(2)点P的纵坐标就是三角形OPA的高,直接写出面积公式.
(3)P,C两点的纵坐标相等,求出C点的横坐标,用m表示PC,再用面积公式.分0<m<6和m<0讨论.
解:(1)将A(-8,0)代入直线y=kx+6,得k=![]() .
.
(2)由题意,得S=![]() OA·y=
OA·y=![]() ×8(
×8(![]() x+6)=3x+24(-8<x<0).
x+6)=3x+24(-8<x<0).
(3)∵PC⊥y轴,P(0,m),∴C点的纵坐标为m.
则![]() x+6=m,
x+6=m,
∴x=![]() .∴C(
.∴C(![]() ,m).∴PC=
,m).∴PC=![]() .
.
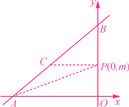
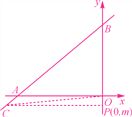
图1 图2
分两种情况:①如图1,当0<m<6时,
S′=![]() OP·PC=
OP·PC=![]() m·
m·![]() =-
=-![]() m2+4m.
m2+4m.
②如图2,当m<0时,
S′=![]() OP·PC=
OP·PC=![]() (-m)·
(-m)·![]() =
=![]() m2-4m.
m2-4m.
综上S′=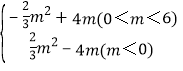 .
.


 百年学典课时学练测系列答案
百年学典课时学练测系列答案 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案科目:初中数学 来源: 题型:
【题目】平面直角坐标系xOy中,点P的坐标为(m+1,m-1).
(1)试判断点P是否在一次函数y=x-2的图象上,并说明理由;
(2)如图,一次函数y=-![]() x+3的图象与x轴、y轴分别相交于A,B,若点P在△AOB的内部,求m的取值范围.
x+3的图象与x轴、y轴分别相交于A,B,若点P在△AOB的内部,求m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系中,O为坐标原点.已知反比例函数y=![]() (k>0)的图象经过点A(2,m),过点A作AB⊥x轴于点B,且△AOB的面积为
(k>0)的图象经过点A(2,m),过点A作AB⊥x轴于点B,且△AOB的面积为![]() .
.
(1)求k和m的值;
(2)求当x≥1时函数值y的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题满分![]() 分)
分)
(![]() )【问题】如图
)【问题】如图![]() ,点
,点![]() 为线段
为线段![]() 外一动点,且
外一动点,且![]() ,
, ![]() .当点
.当点![]() 位于__________时线段
位于__________时线段![]() 的长取得最大值,且最大值为__________(用含
的长取得最大值,且最大值为__________(用含![]() 、
、![]() 的式子表示).
的式子表示).
(![]() )【应用】点
)【应用】点![]() 为线段
为线段![]() 除外一动点,且
除外一动点,且![]() ,
, ![]() .如图
.如图![]() 所示,分别以
所示,分别以![]() 、
、![]() 为边,
为边,
作等边三角形![]() 和等边三角形
和等边三角形![]() ,连接
,连接![]() 、
、![]() .
.
①请找出图中与![]() 相等的线段,并说明理由.
相等的线段,并说明理由.
②直接写出线段![]() 长的最大值.
长的最大值.
(![]() )【拓展】如图
)【拓展】如图![]() ,在平面直角坐标系中,点
,在平面直角坐标系中,点![]() 的坐标为
的坐标为![]() ,点
,点![]() 的坐标为
的坐标为![]() ,点
,点![]() 为线段
为线段
![]() 外一动点,且
外一动点,且![]() ,
, ![]() ,
, ![]() .请直接写出线段
.请直接写出线段![]() 长的最大值及此时点
长的最大值及此时点![]() 的坐标.
的坐标.




查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个多项式加上5x2﹣4x﹣3得﹣x2﹣3x,则这个多项式为( )
A.4x2﹣7x﹣3
B.6x2﹣x﹣3
C.﹣6x2+x+3
D.﹣6x2﹣7x﹣3
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com