
【题目】如图,平行四边形ABCD的顶点C在y轴正半轴上,CD平行于x轴,直线AC交x轴于点E,BC⊥AC,连接BE,反比例函数 ![]() (x>0)的图象经过点D.已知S△BCE=2,则k的值是( )
(x>0)的图象经过点D.已知S△BCE=2,则k的值是( )
A.2
B.﹣2
C.3
D.4
【答案】D
【解析】设D点坐标为(m,n),则AB=CD=m,
∵CD平行于x轴,AB∥CD,
∴∠BAC=∠CEO.
∵BC⊥AC,∠COE=90°,
∴∠BCA=∠COE=90°,
∴△ABC∽△ECO,
∴ ![]() =
= ![]() ,
,
∴BCEC=ABCO=mn.
∵点D在反比例函数y= ![]() 的图象上,
的图象上,
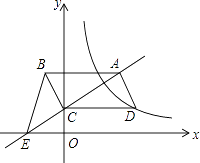
∴k=mn=BCEC=2S△BCE=4.
所以答案是:D.
【考点精析】解答此题的关键在于理解平行四边形的性质的相关知识,掌握平行四边形的对边相等且平行;平行四边形的对角相等,邻角互补;平行四边形的对角线互相平分,以及对相似三角形的判定与性质的理解,了解相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方.


 应用题作业本系列答案
应用题作业本系列答案科目:初中数学 来源: 题型:
【题目】感恩是中华民族的传统美德,在4月份某校提出了“感恩父母、感恩老师、感恩他人”的“三感”教育活动.感恩事例有:A.给父母过一次生日;B .为父母做一次家务活,让父母休息一天;C.给老师一个发自内心的拥抱,并且与老师谈心;D.帮助有困难的同学度过难关.为了解学生对这四种感恩事例的情况,在全校范围内随机抽取若干名学生,进行问卷调查(每个被调查的同学在4种感恩事例中选择最想做的一种),将数据进行整理并绘制成以下两幅统计图(未画完整).
(1)这次调查中,一共查了名学生;
(2)请补全扇形统计图中的数据及条形统计图;
(3)若有3名选 A的学生,1名选 C的学生组成志愿服务队外出参加联谊活动,欲从中随机选出2人担任活动负责人,请通过树状图或列表求两人均是选 A的学生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,M,N分别是边AB、BC的中点,E、F是边AC上的三等分点,连接ME、NF且延长后交于点D,连接BE、BF
(1)求证:四边形BFDE是平行四边形;(2)当△ABC满足什么条件时四边形BFDE是菱形,证明你的结论。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC和△ADE中,边AD与边BC交于点P(不与点B、C重合),点B、E在AD异侧,OA、OC分别是∠PAC和∠PCA的角平分线.


(1)当∠APC =60°时,求∠AOC的度数;
(2)当AB⊥AC,AB=AD=4,AC=3,BC=5时,设AP=x,用含x的式子表示PD,并求PD的最大值;
(3)当AB⊥AC,∠B=20°时,∠AOC的取值范围为α°<∠AOC <β°,直接写出α、β的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点C(﹣3,0),点A,B分别在x轴,y轴的正半轴上,且满足 ![]() +|OA﹣1|=0
+|OA﹣1|=0
(1)求点A,点B的坐标.
(2)若点P从C点出发,以每秒1个单位的速度沿射线CB运动,连结AP.设△ABP的面积为S,点P的运动时间为t秒,求S与t的函数关系式,并写出自变量的取值范围.
(3)在(2)的条件下,是否存在点P,使以点A,B,P为顶点的三角形与△AOB相似?若存在,请直接写出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】点P是平面直角坐标系中的一点且不在坐标轴上,过点P向x轴、y轴作垂线段,若垂线段的长度的和为4,则点P叫做“垂距点”,例如:如图中的点P(1,3)是“垂距点”.
(1)在点A(﹣2,2),![]() ,C(﹣1,5)是“垂距点”是 ;
,C(﹣1,5)是“垂距点”是 ;
(2)若![]() 是“垂距点”,求m的值.
是“垂距点”,求m的值.
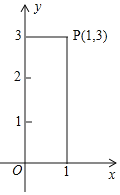
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线PQ∥MN,点C是PQ、MN之间(不在直线PQ,MN上)的一个动点.

(1)若∠1与∠2都是锐角,如图甲,请直接写出∠C与∠1,∠2之间的数量关系;
(2)若把一块三角尺(∠A=30°,∠C=90°)按如图乙方式放置,点D,E,F是三角尺的边与平行线的交点,若∠AEN=∠A,求∠BDF的度数;
(3)将图乙中的三角尺进行适当转动,如图丙,直角顶点C始终在两条平行线之间,点G在线段CD上,连接EG,且有∠CEG=∠CEM,求![]() 值.
值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在![]() 中,AB,BC,AC三边的长分别为
中,AB,BC,AC三边的长分别为![]() 、
、![]() 、
、![]() ,求这个三角形的面积
,求这个三角形的面积![]() 小辉同学在解答这道题时,先建立一个正方形网格
小辉同学在解答这道题时,先建立一个正方形网格![]() 每个小正方形的边长为
每个小正方形的边长为![]() ,再在网格中画出格点
,再在网格中画出格点![]() 的三个顶点都在正方形的顶点处
的三个顶点都在正方形的顶点处![]() ,如图所示,这样不需要求
,如图所示,这样不需要求![]() 的高,而借用网格就能计算出它的面积.
的高,而借用网格就能计算出它的面积.
![]() 请你将
请你将![]() 的面积直接填写在横线上.______
的面积直接填写在横线上.______
![]() 已知
已知![]() ,DE、EF、DF三边的长分别为
,DE、EF、DF三边的长分别为![]() 、
、![]() 、
、![]() ,
,
![]() 是否为直角形,并说明理由.
是否为直角形,并说明理由.
![]() 求这个三角形的面积.
求这个三角形的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx﹣4与x轴交于A(4,0)、B(﹣2,0)两点,与y轴交于点C,点P是线段AB上一动点(端点除外),过点P作PD∥AC,交BC于点D,连接CP.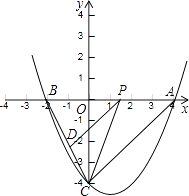
(1)求该抛物线的解析式;
(2)当动点P运动到何处时,BP2=BDBC;
(3)当△PCD的面积最大时,求点P的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com