
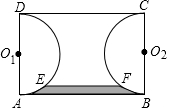
 如图,已知矩形ABCD中,AB=3,AD=2,分别以边AD,BC为直径在矩形ABCD的内部作半圆O1和半圆O2,一平行于AB的直线EF与这两个半圆分别交于点E、点F,且EF=2(EF与AB在圆心O1和O2的同侧),则由$\widehat{AE}$,EF,$\widehat{FB}$,AB所围成图形(图中阴影部分)的面积等于3-$\frac{5\sqrt{3}}{4}$-$\frac{π}{6}$.
如图,已知矩形ABCD中,AB=3,AD=2,分别以边AD,BC为直径在矩形ABCD的内部作半圆O1和半圆O2,一平行于AB的直线EF与这两个半圆分别交于点E、点F,且EF=2(EF与AB在圆心O1和O2的同侧),则由$\widehat{AE}$,EF,$\widehat{FB}$,AB所围成图形(图中阴影部分)的面积等于3-$\frac{5\sqrt{3}}{4}$-$\frac{π}{6}$. 分析 连接O1O2,O1E,O2F,过E作EG⊥O1O2,过F⊥O1O2,得到四边形EGHF是矩形,根据矩形的性质得到GH=EF=2,求得O1G=$\frac{1}{2}$,得到∠O1EG=30°,根据三角形、梯形、扇形的面积公式即可得到结论.
解答 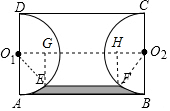 解:连接O1O2,O1E,O2F,
解:连接O1O2,O1E,O2F,
则四边形O1O2FE是等腰梯形,
过E作EG⊥O1O2,过FH⊥O1O2,
∴四边形EGHF是矩形,
∴GH=EF=2,
∴O1G=$\frac{1}{2}$,
∵O1E=1,
∴GE=$\frac{\sqrt{3}}{2}$,
∴$\frac{{O}_{1}G}{{O}_{1}E}$=$\frac{1}{2}$;
∴∠O1EG=30°,
∴∠AO1E=30°,
同理∠BO2F=30°,
∴阴影部分的面积=S${\;}_{矩形AB{O}_{2}{O}_{1}}$-2S${\;}_{扇形A{O}_{1}E}$-S${\;}_{梯形EF{O}_{2}{O}_{1}}$=3×1-2×$\frac{30•π×{1}^{2}}{360}$-$\frac{1}{2}$(2+3)×$\frac{\sqrt{3}}{2}$=3-$\frac{5\sqrt{3}}{4}$-$\frac{π}{6}$.
故答案为:3-$\frac{5\sqrt{3}}{4}$-$\frac{π}{6}$.
点评 本题考查了扇形面积的计算,矩形的性质,梯形的性质,正确的作出辅助线是解题的关键.


 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案科目:初中数学 来源: 题型:解答题
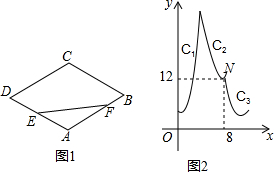 如图1,在菱形ABCD中,点E为AD的中点,点F为折线A-B-C-D上一个动点(从点A出发到点D停止),连结EF,设点F的运动路径的长为x,EF2为y,y关于x的函数图象由C1,C2,C3三段组成,已知C2与C3的界点N的坐标如图2所示.
如图1,在菱形ABCD中,点E为AD的中点,点F为折线A-B-C-D上一个动点(从点A出发到点D停止),连结EF,设点F的运动路径的长为x,EF2为y,y关于x的函数图象由C1,C2,C3三段组成,已知C2与C3的界点N的坐标如图2所示.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. |  | B. |  | ||
| C. |  | D. |  |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com