
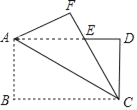
【题目】如图,将长方形ABCD沿对角线AC翻折,点B落在点F处,FC交AD于点E,若AB=4,BC=8,则△ACE的面积为_____.
【答案】10
【解析】
利用折叠的性质可得出AF,CF的值及∠ACF=∠ACB,由AD∥BC,可得出∠CAD=∠ACF,进而可得出AE=CE,设AE=x,则EF=8﹣x,在Rt△AEF中,利用勾股定理可求出x的值,再利用三角形的面积公式即可求出△ACE的面积.
由折叠的性质,可知:AF=AB=4,CF=CB=8,∠F=∠B=90°,∠ACF=∠ACB.
∵AD∥BC,
∴∠CAD=∠ACB,
∴∠CAD=∠ACF,
∴AE=CE.
设AE=x,则EF=8﹣x.
在Rt△AEF中,AF=4,AE=x,EF=8﹣x,∠F=90°,
∴42+(8﹣x)2=x2,
∴x=5,
∴S△ACE=![]() AEAB=
AEAB=![]() ×5×4=10.
×5×4=10.
故答案为:10.


科目:初中数学 来源: 题型:
【题目】如图,已知l1∥l2,MN分别和直线l1、l2交于点A、B,ME分别和直线l1、l2交于点C、D,点P在MN上(P点与A、B、M三点不重合).
(1)如果点P在A、B两点之间运动时,∠α、∠β、∠γ之间有何数量关系请说明理由;
(2)如果点P在A、B两点外侧运动时,∠α、∠β、∠γ有何数量关系(只须写出结论).

查看答案和解析>>
科目:初中数学 来源: 题型:
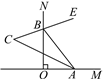
【题目】如图,∠MON=90°,点A,B分别在射线OM,ON上运动,BE平分∠ABN,BE的反向延长线与∠BAO的平分线交于点C.
(1)当点A,B移动后,∠BAO=45°时,∠C=________;
(2)当点A,B移动后,∠BAO=60°时,∠C=________;
(3)由(1)(2)猜想∠C是否随点A,B的移动而发生变化,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)发现:如图1,点A为线段BC外一动点,且BC=a,AB=b.
填空:当点A位于 时,线段AC的长取得最大值,且最大值为 (用含a、b的式子表示);
(2)应用:点A为线段BC外一动点,且BC=4,AB=2,如图2,分别以AB、AC为边,作等边三角形ABD和等边△ACE,连接CD、BE.
①请找出图中与BE相等的线段,并说明理由;
②直接写出线段BE长的最大值;
③直接写出△DBC面积的最大值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的袋子里装有8个红球,4个黄球,3个白球,他们除了颜色外都相同,两人做游戏,游戏规则如下:一个人抓住袋子,一个人摸球,若摸出红球,摸球者胜,否则拿袋子的人获胜.
(1)如果你参加游戏,为了尽可能的获胜,你是做摸球的人还是做拿袋子的人?为什么?
(2)你说这个游戏公平吗?如果公平,说明理由:如果不公平,请给出修改建议,使它对双方都是公平的.
查看答案和解析>>
科目:初中数学 来源: 题型:
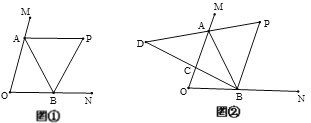
【题目】如图①,∠MON=70°,点A、B在∠MON的两条边上运动,∠MAB与∠NBA的平分线交于点P.
(1)点A、B在运动过程中,∠P的大小会变吗?如果不会,求出∠P的度数;如果会,请说明理由.
(2)如图②,继续作BC是平分![]() ,AP的反向延长线交BC的延长线于点D,点A、B在运动过程中,∠D的大小会变吗?如果不会,求出∠D的度数;如果会,请说明理由.
,AP的反向延长线交BC的延长线于点D,点A、B在运动过程中,∠D的大小会变吗?如果不会,求出∠D的度数;如果会,请说明理由.
(3)如图②,∠P和∠D有怎样的数量关系?(直接写出答案)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】经过建设者三年的努力,贯穿四川的“遂内高速”正式通车,已知原来从遂宁到内江的公路长150km,高速公路路程比公路缩短30km,一辆小车从遂宁到内江走高速公路的平均速度可以提高到原来的1.5倍,用时比原来减少1小时,求小车原来的平均速度和走高速的平均速度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,小明准备测量一段水渠的深度,他把一根竹竿AB竖直插到水底,此时竹竿AB离岸边点C处的距离![]() 米。竹竿高出水面的部分AD长0.5米,如果把竹竿的顶端A拉向岸边点C处,竿顶和岸边的水面刚好相齐,则水渠的深度BD为( )
米。竹竿高出水面的部分AD长0.5米,如果把竹竿的顶端A拉向岸边点C处,竿顶和岸边的水面刚好相齐,则水渠的深度BD为( )

A. 2米B. 2.5米C. 2.25米D. 3米
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com