
����Ŀ����ͼ����ʾ����Բ���������ڷ���һ��ʵ�ĵġ����塱����һ��Բ����һ��ͬ�����Բ��ɵļ����壩�������������������עˮ��ˮ���ٶ�Ϊ5cm3/s��ע��Ϊֹ����֪����עˮ�����У�ˮ��߶�h��cm����עˮʱ��t��s��֮��Ĺ�ϵ��ͼ����ʾ���������ͼ����Ϣ������������⣺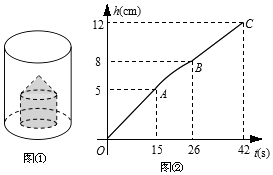
��1��Բ���������ĸ�Ϊcm�������塱��Բ��ĸ�Ϊcm��
��2���ֱ����Բ���������ĵ�����롰���塱�ĵ������

| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������С��ͬѧ����һ������
�ⷽ����![]()
������ȥ��ĸ���� 4��2x��1��=1��3��x+2��
��ȥ�������� 8x��4=1��3x��6
����������8x+3x=1��6+4
���ϲ�ͬ�������� 11x=��1
��ϵ����Ϊ1����![]()
��1������Ľ��������������ִ���IJ����ǣ�����ţ� ��
��2�����ڱ����ұ���ȷ�Ľⷽ����![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��1������AOB=45�㣬��P��Q�ֱ��DZ�OA��OB�ϵ����㣬��OP=2cm������O��PQ�۵�����O����ƽ���ڵ�C����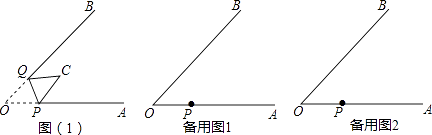
��1����PC��QBʱ��OQ=��
��2����PC��QBʱ����OQ�ij���
��3�����۵����ص�����Ϊ����������ʱ����OQ�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵxOy�У�һ�κ���y=kx+b��ͼ���뷴��������y=![]() ��ͼ���ཻ�ڵ�A��m��3����B����6��n������x�ύ�ڵ�C��
��ͼ���ཻ�ڵ�A��m��3����B����6��n������x�ύ�ڵ�C��
��1����һ�κ���y=kx+b�Ĺ�ϵʽ��
��2�����ͼ��ֱ��д������kx+b��![]()
![]() ��x��ȡֵ��Χ��
��x��ȡֵ��Χ��
��3������P��x���ϣ���S��ACP=![]() S��BOC�����P�����꣮
S��BOC�����P�����꣮

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ABC�У�AB=CB����ABC=90�㣬DΪAB�ӳ�����һ�㣬��E��BC���ϣ���BE=BD������AE��DE��DC�� ����֤����ABE�ա�CBD��
������CAE=30�㣬���BDC�Ķ�����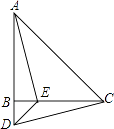
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪�������չ��ͼ��ͼ��ʾ������������������ֱ�����ĸA��B��C��D��E��F��ʾ���������ϵ����ֱ��������������Ϊ�෴����������B=1��C=��a2��2a+1��D=��1��E=3a+4��F=2��aʱ����A���ʾ����ֵ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ����A�ǰ�Բ��һ�����ȷֵ㣬��B�� ![]() ���е㣬��P��ֱ�� MN��һ���㣬����O��ֱ��Ϊ2����AP+BP����Сֵ�� ��
���е㣬��P��ֱ�� MN��һ���㣬����O��ֱ��Ϊ2����AP+BP����Сֵ�� �� 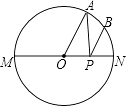
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ʯ���ڴ������Ҽ��������������У��̻����β���������ijУ�ƻ�����A��B������ľ��100�ý���У�̻����������г����飺����A����ľ2�ã�B����ľ5�ã�����600Ԫ������A����ľ3�ã�B����ľ1�ã�����380Ԫ��
��1����A�֣�B����ľÿ�ø�����Ԫ��
��2������Ҫ������A����ľ������������B����ľ������3����ѧУ���б깫˾ǩ���ĺ�ͬ�й涨�����г��۸������£��������������أ���ʵ�ʸ����ܽ��г��۾����Żݣ������һ�ֹ�����ľ�ķ�����ʹʵ������������ʡ���������ʡ�ķ��ã�
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com