
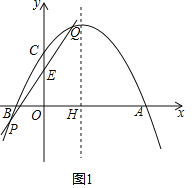
【题目】如图,在平面直角坐标系中,抛物线y=ax2+bx+c的图象与x轴交于A(4,0),B两点,与y轴交于点C(0,2),对称轴x=1,与x轴交于点H.

(1)求抛物线的函数表达式;
(2)直线y=kx+1(k≠0)与y轴交于点E,与抛物线交于点 P,Q(点P在y轴左侧,点Q在y轴右侧),连接CP,CQ,若△CPQ的面积为![]() ,求点P,Q的坐标;
,求点P,Q的坐标;
(3)在(2)的条件下,连接AC交PQ于G,在对称轴上是否存在一点K,连接GK,将线段GK绕点G顺时针旋转90°,使点K恰好落在抛物线上,若存在,请直接写出点K的坐标;若不存在,请说明理由.
【答案】(1)y=![]() ;(2)点P、Q的坐标分别为:(
;(2)点P、Q的坐标分别为:(![]() ,
,![]() )、(
)、(![]() ,﹣
,﹣![]() );(3)存在,点K(1,
);(3)存在,点K(1,![]() ).
).
【解析】
(1)根据对称轴x=1,求出点B的坐标,再将点B代入抛物线表达式中求出a的值,即可求抛物线的函数表达式;
(2)设直线PQ交y轴于点E(0,1),点P、Q横坐标分别为m,n,联立抛物线与直线PQ的表达式可得方程,求解方程即可得出点P,Q的坐标;
(3)设点K(1,m),联立PQ和AC的表达式,即可求出G点的坐标,过点G作x轴的平行线交函数对称轴于点M,交过点R与y轴的平行线于点N,通过△KMG≌△GNR可得R(m﹣1,![]() ),将R点代入抛物线解析式即可求出m的值,求得K的坐标.
),将R点代入抛物线解析式即可求出m的值,求得K的坐标.
(1)对称轴x=1,则点B(﹣2,0),
则抛物线的表达式为:y=a(x+2)(x﹣4)=a(x2﹣2x﹣8),
即﹣8a=2,
解得:a=![]() ,
,
故抛物线的表达式为:y=![]() ;
;
(2)设直线PQ交y轴于点E(0,1),点P、Q横坐标分别为m,n,
△CPQ的面积=![]() ×CE×(n﹣m)=
×CE×(n﹣m)=![]() ,即n﹣m=2
,即n﹣m=2![]() ,
,
联立抛物线与直线PQ的表达式并整理得:![]() …①,
…①,
m+n=2﹣4k,mn=﹣4,
n﹣m=2![]() =
=![]() =
=![]() ,
,
解得:k=0(舍去)或1;
将k=1代入①式并解得:x=![]() ,
,
故点P、Q的坐标分别为:(![]() ,
,![]() )、(
)、(![]() ,﹣
,﹣![]() )
)
(3)设点K(1,m),
联立PQ和AC的表达式并解得:x=![]() ,故点G(
,故点G(![]() ,
,![]() )
)
过点G作x轴的平行线交函数对称轴于点M,交过点R与y轴的平行线于点N,
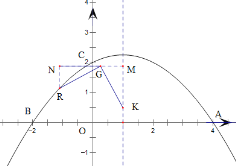
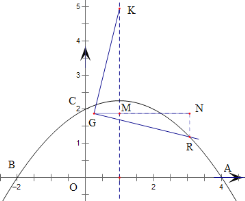
则△KMG≌△GNR(AAS),
GM=1-![]() =
=![]() =NR,MK=
=NR,MK=![]() ,
,
故点R的纵坐标为:![]() ,则点R(m﹣1,
,则点R(m﹣1,![]() )
)
将该坐标代入抛物线表达式解得:x=![]() ,
,
故m=![]() ,
,
故点K(1,![]() ).
).


 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案科目:初中数学 来源: 题型:
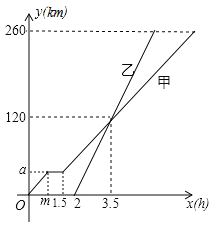
【题目】甲、乙两车都从A地驶向B地,并以各自的速度匀速行驶![]() 甲车比乙车早行驶,甲车途中休息了
甲车比乙车早行驶,甲车途中休息了![]() 设甲车行驶时间为
设甲车行驶时间为![]() ,下图是甲乙两车行驶的距离
,下图是甲乙两车行驶的距离![]() 与
与![]() 的函数图象,根据题中信息回答问题:
的函数图象,根据题中信息回答问题:
![]() 填空:
填空:![]() ______,
______,![]() ______;
______;
![]() 当乙车出发后,求乙车行驶路程
当乙车出发后,求乙车行驶路程![]() 与
与![]() 的函数解析式,并写出相应的x的取值范围;
的函数解析式,并写出相应的x的取值范围;
![]() 当甲车行驶多长时间时,两车恰好相距50km?请直接写出答案.
当甲车行驶多长时间时,两车恰好相距50km?请直接写出答案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,抛物线![]() 与
与![]() 轴交于
轴交于![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() ,
,![]() ,矩形
,矩形![]() 的边
的边![]() ,延长
,延长![]() 交抛物线于点
交抛物线于点![]() .
.
(1)求抛物线的表达式;
(2)如图2,点![]() 是直线
是直线![]() 上方抛物线上的一个动点,过点
上方抛物线上的一个动点,过点![]() 作
作![]() 轴的平行线交直线
轴的平行线交直线![]() 于点
于点![]() ,作
,作![]() ,垂足为
,垂足为![]() .设
.设![]() 的长为
的长为![]() ,点
,点![]() 的横坐标为
的横坐标为![]() ,求
,求![]() 与
与![]() 的函数关系是(不必写出
的函数关系是(不必写出![]() 的取值范围),并求出
的取值范围),并求出![]() 的最大值;
的最大值;
(3)如果点![]() 是抛物线对称轴上的一点,抛物线上是否存在点
是抛物线对称轴上的一点,抛物线上是否存在点![]() ,使得以
,使得以![]() 为顶点的四边形是平行四边形?若存在,直接写出所有满足条件的
为顶点的四边形是平行四边形?若存在,直接写出所有满足条件的![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=ax2+bx+c(a≠0)的顶点D坐标为(2,﹣1),且过点B(3,0),与y轴交于点C.
(1)求抛物线的解析式及点C的坐标;
(2)连结OD、CD、CB,CD交x轴于点E,求S△CEB:S△ODE.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学计划根据学生的兴趣爱好组建课外兴趣小组,并随机抽取了部分同学的兴趣爱好进行调查,将收集的数据整理并绘制成下列两幅统计图,请根据图中的信息,完成下列问题:
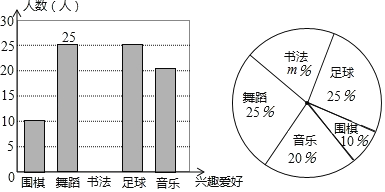
![]() 学校这次调查共抽取了 名学生;
学校这次调查共抽取了 名学生;
![]() 求
求![]() 的值并补全条形统计图;
的值并补全条形统计图;
![]() 在扇形统计图中,“围棋”所在扇形的圆心角度数为 ;
在扇形统计图中,“围棋”所在扇形的圆心角度数为 ;
![]() 设该校共有学生
设该校共有学生![]() 名,请你估计该校有多少名学生喜欢足球.
名,请你估计该校有多少名学生喜欢足球.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的袋子中装有大小、形状完全相同的三个小球,上面分别标有1,2,3三个数字.
(1)从中随机摸出一个球,求这个球上数字是奇数的概率是 ;
(2)从中先随机摸出一个球记下球上数字,然后放回洗匀,接着再随机摸出一个,求这两个球上的数都是奇数的概率(用列表或树状图方法)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(8分)如图,已知O是坐标原点,B、C两点的坐标分别为(3,-1)、(2,1)。

(1)以O点为位似中心在y轴的左侧将△OBC放大到两倍画出图形。
(2)写出B、C两点的对应点B、C的坐标;
(3)如果△OBC内部一点M的坐标为(x,y),写出M的对应点M的坐标。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com