
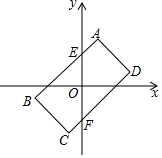
 如图,四边形ABCD是以原点O为对称中心的矩形,A(1,3),D(3,1),AB和CD分别与y轴交于点E、F,连接OB.
如图,四边形ABCD是以原点O为对称中心的矩形,A(1,3),D(3,1),AB和CD分别与y轴交于点E、F,连接OB.分析 (1)由O为对称中心可知,A和C、B和D关于原点对称,可求得B、C的坐标;
(2)由C、D坐标可求得直线CD的解析式,可求得F点坐标,再利用勾股定理可求得BC、CD、CF的长,过O作OM⊥CD、ON⊥BC,垂足分别为M、N,则可求得△BOC和COF的面积,可求得四边形OBCF的面积;
(3)把x=1代入(2)中直线CD的解析式可求得对应的y值,与-0.8进行比较即可;
(4)当直线过A点和C点时直线与矩形有一个公共点,可求得没有公共点时m的取值范围.
解答 解:
(1)∵四边形ABCD是以原点O为对称中心的矩形,
∴A和C、B和D关于原点对称,
∴B(-3,-1),C(-1,-3);
(2)设直线CD的解析式为y=kx+b,
∴$\left\{\begin{array}{l}{3k+b=1}\\{-k+b=-3}\end{array}\right.$,解得$\left\{\begin{array}{l}{k=1}\\{b=-2}\end{array}\right.$,
∴直线CD解析式为y=x-2,
∴F(0,-2),
∵B(-3,-1),C(-1,-3),D(3,1),
∴BC=$\sqrt{(-3+1)^{2}+(-1+3)^{2}}$=2$\sqrt{2}$,CF=$\sqrt{(-1-0)^{2}+(-3+2)^{2}}$=$\sqrt{2}$,CD=$\sqrt{(-1-3)^{2}+(-3-1)^{2}}$=4$\sqrt{2}$,
过O作OM⊥CD、ON⊥BC,垂足分别为M、N,如图,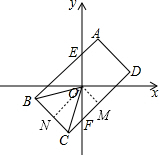
∵四边形ABCD为矩形,
∴OM=$\frac{1}{2}$BC=$\sqrt{2}$,ON=$\frac{1}{2}$CD=2$\sqrt{2}$,
∴S四边形OBCF=S△OBC+S△OCF=$\frac{1}{2}$BC•ON+$\frac{1}{2}$CF•OM=$\frac{1}{2}$×2$\sqrt{2}$×2$\sqrt{2}$+$\frac{1}{2}$×$\sqrt{2}$×$\sqrt{2}$=5;
(3)在y=x-2中,当x=1时可得y=-1,
∵-0.8>-1,
∴点(1,-0.8)在点(1,-1)的上方,
即点(1,-0.8)在矩形的内部;
(4)当直线y=$\frac{1}{2}$x+m过A、C点时,直线与矩形只有一个公共点,
把A(1,3)代入可得3=$\frac{1}{2}$+m,解得m=$\frac{5}{2}$,
把C(-1,-3)代入可得-3=-$\frac{1}{2}$+m,解得m=-$\frac{5}{2}$,
∴当直线y=$\frac{1}{2}$x+m与矩形ABCD没有公共点,m的取值范围为m<-$\frac{5}{2}$或m>$\frac{5}{2}$.
点评 本题为一次函数的综合应用,涉及矩形的性质、待定系数法、勾股定理、三角形的面积等知识.在(1)中利用矩形的对称性容易求得B、C的坐标,在(2)中把四边形转化成两个三角形是解题的关键,在(3)中判断出点在CD的上方还是下方是解题的关键,在(4)中求得直线与矩形有一个公共点时m的值是解题的关键.本题考查知识点较多,综合性较强,难度适中.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:选择题
| A. | 若|x|=|y|,则x=y | B. | 若x2=y2,则x=y | C. | 若$\sqrt{x^2}=|y|$,则x=y | D. | 若$\root{3}{x}=\root{3}{y}$,则x=y |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
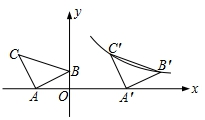 如图,在平面直角坐标系中有Rt△ABC,已知∠CAB=90°,AB=AC,A(-2,0),B(0,1).
如图,在平面直角坐标系中有Rt△ABC,已知∠CAB=90°,AB=AC,A(-2,0),B(0,1).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
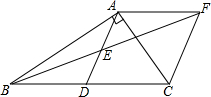 如图,在△ABC中,∠BAC=90°,AD是中线,E是AD的中点,过点A作AF∥BC交BE的延长线于F,连接CF,求证:四边形ADCF是菱形.
如图,在△ABC中,∠BAC=90°,AD是中线,E是AD的中点,过点A作AF∥BC交BE的延长线于F,连接CF,求证:四边形ADCF是菱形.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 高铁给我们的出行带来了极大的方便.如图,“和谐号”高铁列车座椅后面的小桌板收起时,小桌板的支架的底端N与桌面顶端M的距离MN=75cm,且可以看作与地面垂直.展开小桌板使桌面保持水平,AB⊥MN,∠MAB=∠MNB=37°,且支架长BN与桌面宽AB的长度之和等于MN的长度.求小桌板桌面的宽度AB(结果精确到1cm,参考数据:sin37°≈0.6,cos37°≈0.8,tan37°≈0.75)
高铁给我们的出行带来了极大的方便.如图,“和谐号”高铁列车座椅后面的小桌板收起时,小桌板的支架的底端N与桌面顶端M的距离MN=75cm,且可以看作与地面垂直.展开小桌板使桌面保持水平,AB⊥MN,∠MAB=∠MNB=37°,且支架长BN与桌面宽AB的长度之和等于MN的长度.求小桌板桌面的宽度AB(结果精确到1cm,参考数据:sin37°≈0.6,cos37°≈0.8,tan37°≈0.75)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
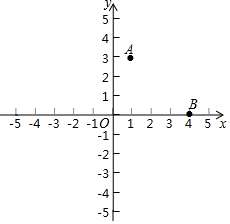 定义[p,q]为一次函数y=px+q的特征数.
定义[p,q]为一次函数y=px+q的特征数.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com