
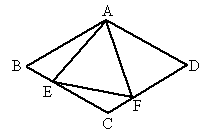
如图所示,在菱形ABCD中,E、F分别是BC、CD上的点,∠B=∠EAF=60°,∠BAE=18°,求∠CEF的度数.
|
解:连接 AC.由菱形ABCD有BA=BC,∠B+∠BAD=180°.因为∠ =60°,所以△ABC是等边三角形,所以∠BAD=120°,又因为∠ BAE+∠FAD+∠FAD=120°,所以∠ FAD=120°-18°-60°=42°.又因为△ ACD是等边三角形,所以∠CAD=60°,所以∠ CAF=60°-42°=18°,所以上∠ BAE=∠CAF,在△ BAE和△CAF中,AB=AC,∠B=∠ACF=60°,∠BAE=∠CAF,所以△ BAE≌△CAF,所以AE=AF,而△EAF=60°.所以△ AEF是等边三角形,所以∠AEF=60°.在△ AEB中,∠AEB=180°-∠B-∠BAE=180°-60°-18°=102°.又因为∠ AEB+∠AED+∠CEF=180°,所以∠ CEF=180°-102°-60°=18°. |
|
连接 AC,可得△ABC为正三角形,易得∠BAE=∠CAF,△BAE≌△CAF.推出△AEF为等边三角形,则∠CEF的度数即可求得.关键证出△ AEF是等边三角形. |


 同步练习强化拓展系列答案
同步练习强化拓展系列答案科目:初中数学 来源: 题型:
 如图所示,在菱形ABCD中,AC,BD交于点O,AB=15,AO=12,P从A出发,Q从O出发,分别以2cm/s和1cm/s的速度各自向O,B点运动,当运动时间为多少秒时,四边形BQPA的面积是△POQ面积的8倍.
如图所示,在菱形ABCD中,AC,BD交于点O,AB=15,AO=12,P从A出发,Q从O出发,分别以2cm/s和1cm/s的速度各自向O,B点运动,当运动时间为多少秒时,四边形BQPA的面积是△POQ面积的8倍.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com