
【题目】如图,已知一次函数y=kx+b的图象与反比例函数![]() 的图象交于A,B两点,且点A的横坐标和点B的纵坐标都是﹣2,
的图象交于A,B两点,且点A的横坐标和点B的纵坐标都是﹣2,
求:(1)一次函数的解析式;
(2)△AOB的面积;
(3)直接写出一次函数的函数值大于反比例函数的函数值时x的取值范围.
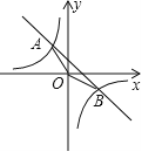
【答案】(1)一次函数的解析式为y=﹣x+2;(2)S△AOB=6;(3)由图象可知:一次函数的函数值大于反比例函数的函数值时x的取值范围是x<﹣2或0<x<4.
【解析】试题分析:(1)由点A、B的横纵坐标结合反比例函数解析式即可得出点A、B的坐标,再由点A、B的坐标利用待定系数法即可得出直线AB的解析式;
(2)设直线AB与y轴交于C,找出点C的坐标,利用三角形的面积公式结合A、B点的横坐标即可得出结论;
(3)观察函数图象,根据图象的上下关系即可找出不等式的解集.
试题解析:(1)令反比例函数y=-![]() 中x=-2,则y=4,
中x=-2,则y=4,
∴点A的坐标为(-2,4);
反比例函数y=-![]() 中y=-2,则-2=-
中y=-2,则-2=-![]() ,解得:x=4,
,解得:x=4,
∴点B的坐标为(4,-2).
∵一次函数过A、B两点,
∴![]() ,解得:
,解得: ![]() ,
,
∴一次函数的解析式为y=-x+2.
(2)设直线AB与y轴交于C,
令为y=-x+2中x=0,则y=2,
∴点C的坐标为(0,2),
∴S△AOB=![]() OC(xB-xA)=
OC(xB-xA)=![]() ×2×[4-(-2)]=6.
×2×[4-(-2)]=6.
(3)观察函数图象发现:
当x<-2或0<x<4时,一次函数图象在反比例函数图象上方,
∴一次函数的函数值大于反比例函数的函数值时x的取值范围为x<-2或0<x<4.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】一个人从A地出发向北偏东80°方向到达B地,再从B地向北偏西25°方向到达C地,如果∠ACB=55°,则∠CAB的度数是( )
A. 25° B. 50° C. 70° D. 75°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列四组线段中,能组成直角三角形的是( )
A. a=2,b=4,c=6B. a=4,b=6,c=8
C. a=4,b=8,c=10D. a=6,b=8,c=10
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】线段CD是由线段AB平移得到的,点A(1,4)的对应点为点C(4,7),则点B(4,1)的对应点D的坐标为( )
A. (7,4) B. (5,3) C. (2,9) D. (1,2)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将100个数据分成①-⑧组,如下表所示:
组号 | ① | ② | ③ | ④ | ⑤ | ⑥ | ⑦ | ⑧ |
频数 | 4 | 8 | 12 | 24 | 18 | 7 | 3 |
那么第④组的频率为( )
A. 0.24B. 0.26C. 24D. 26
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com