
【题目】同学们知道:“在直角三角形中,如果一条直角边等于斜边的一半,那么这条直角边所对的锐角等于30°.”
(1)请写出它的逆命题 ;该逆命题是一个 命题(填“真”或“假”)
(2)若你的判断是真命题请写出证明过程(要求画图,并写出已知,求证).若是假命题,请说明理由.
【答案】(1)在直角三角形中,如果一个锐角等于30度,那么它所对的直角边等于斜边的一半,真;(2)已知,在Rt△ABC中,∠A=30°,∠ACB=90°.求证:BC=![]() AB.
AB.
【解析】
(1)写出逆命题,并判断是真命题;
(2)首先写出已知、求证,画出图形,借助等边三角形的判定和性质证明或借助三角形的外接圆证明.
解:(1)原命题的逆命题为:在直角三角形中,如果一个锐角等于30度,那么它所对的直角边等于斜边的一半,该逆命题是一个真命题;
(2)已知,在Rt△ABC中,∠A=30°,∠ACB=90°.
求证:BC=![]() AB.
AB.
证明:
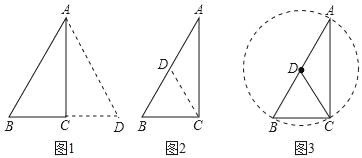
证法一:如图1所示,延长BC到D,使CD=BC,连接AD,易证AD=AB,∠BAD=60°.
∴△ABD为等边三角形,
∴AB=BD,
∴BC=CD=![]() AB,即BC=
AB,即BC=![]() AB.
AB.
证法二:如图2所示,取AB的中点D,
连接DC,有CD=![]() AB=AD=DB,
AB=AD=DB,
∴∠DCA=∠A=30°,∠BDC=∠DCA+∠A=60°.
∴△DBC为等边三角形,
∴BC=DB=![]() AB,即BC=
AB,即BC=![]() AB.
AB.
证法三:如图3所示,在AB上取一点D,使BD=BC,
∵∠B=60°,
∴△BDC为等边三角形,
∴∠DCB=60°,∠ACD=90°﹣∠DCB=90°﹣60°=30°=∠A.
∴DC=DA,即有BC=BD=DA=![]() AB,
AB,
∴BC=![]() AB.
AB.
证法四:如图3所示,作△ABC的外接圆⊙D,∠C=90°,AB为⊙O的直径,
连DC,有DB=DC,∠BDC=2∠A=2×30°=60°,
∴△DBC为等边三角形,
∴BC=DB=DA=![]() AB,即BC=
AB,即BC=![]() AB.
AB.


 走进文言文系列答案
走进文言文系列答案科目:初中数学 来源: 题型:
【题目】如图,一次函数y=kx+b的图象与反比例函数 ![]() 的图象交于A(﹣2,1),B(1,n)两点.
的图象交于A(﹣2,1),B(1,n)两点.
(1)试确定上述反比例函数和一次函数的表达式;
(2)求△AOB的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图1,将两块直角三角尺的直角顶点C叠放在一起,若∠DCE=35°,则∠ACB=_____;若∠ACB=140°,则∠DCE=_______;
(2)猜想∠ACB与∠DCE的大小有何特殊关系,并说明理由;
(3)如图2,若是两个同样的直角三角尺60°锐角的顶点A重合在一起,则∠DAB与∠CAE的大小又有何关系,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,边长为1的正方形ABCD中,点E在CB的延长线上,连接ED交AB于点F,AF=x(0.2≤x≤0.8),EC=y.则在下面函数图象中,大致能反映y与x之间函数关系的是( )
A.
B.
C.
D.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把四张形状大小完全相同的小长方形卡片(如图①)不重叠地放在一个底面为长方形(长为m,宽为n)的盒子底部(如图②),盒子底面未被卡片覆盖的部分用阴影表示.则图②中两块阴影部分的周长和是( )

A. 4nB. 4mC. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】直线y=kx+b与反比例函数y= ![]() (x<0)的图象交于点A(﹣1,m),与x轴交于点B(1,0)
(x<0)的图象交于点A(﹣1,m),与x轴交于点B(1,0)
(1)求m的值;
(2)求直线AB的解析式;
(3)若直线x=t(t>1)与直线y=kx+b交于点M,与x轴交于点N,连接AN,S△AMN= ![]() ,求t的值.
,求t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,现有5张写着不同数字的卡片,请按要求完成下列问题:
![]()
![]() 若从中取出2张卡片,使这2张卡片上数字的乘积最大,则乘积的最大值是______.
若从中取出2张卡片,使这2张卡片上数字的乘积最大,则乘积的最大值是______.
![]() 若从中取出2张卡片,使这2张卡片上数字相除的商最小,则商的最小值是______.
若从中取出2张卡片,使这2张卡片上数字相除的商最小,则商的最小值是______.
![]() 若从中取出4张卡片,请运用所学的计算方法,写出两个不同的运算式,使四个数字的计算结果为24.
若从中取出4张卡片,请运用所学的计算方法,写出两个不同的运算式,使四个数字的计算结果为24.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com