
【题目】阅读下列材料,然后解答后面的问题。
我们知道方程![]() 有无数组解,但在实际生活中我们往往只需要求出其正整数解。例:由
有无数组解,但在实际生活中我们往往只需要求出其正整数解。例:由![]() ,得
,得![]() ,(
,( ![]() 、
、![]() 为正整数)
为正整数)
![]() 则有
则有![]() .又
.又![]() 为正整数,则
为正整数,则![]() 为整数.
为整数.
由2与3互质,可知: ![]() 为3的倍数,从而
为3的倍数,从而![]() ,代入
,代入![]() .
.
![]() 的正整数解为
的正整数解为![]()
问题:(1)若![]() 为自然数,则满足条件的
为自然数,则满足条件的![]() 值有_____________个
值有_____________个
(2)请你写出方程![]() 的所有正整数解:_________________________
的所有正整数解:_________________________
(3)若![]() ,请用含
,请用含![]() 的式子表示
的式子表示![]() ,并求出它的所有整数解。
,并求出它的所有整数解。
【答案】 (1)4 (2) ![]() ,
, ![]() ) (3)
) (3) ![]()
![]()
![]()
![]()
【解析】根据已知代数式为自然数,确定出x的值即可;
(2)用x表示出y,确定出方程的正整数解即可;
(3)用x表示出y,确定出方程的整数解即可.
解:(1)由题意得:x2=1,x2=2,x2=3,x2=6,
解得:x=3,x=4,x=5,x=8,共4个;
故答案为:4;
(2)方程整理得:y=2x+5,
当x=1时,y=3;当x=2时,y=1,
则方程的正整数解为![]() ,
, ![]() ;
;
故答案为: ![]() ,
, ![]()
(3)根据题意得:y=![]() ,
,
根据题意得:x+3=1,x+3=2,x+3=4,x+3=8,
解得:x=2,x=1,x=1,x=5,
相应的y=8,y=4,y=2,y=1,
∴它的所有整数解为![]()
![]()
![]()
![]() .
.


 华东师大版一课一练系列答案
华东师大版一课一练系列答案 孟建平名校考卷系列答案
孟建平名校考卷系列答案科目:初中数学 来源: 题型:
【题目】如图,CD是△ABC的角平分线,AE⊥CD于E,F是AC的中点,
(1)求证:EF∥BC;
(2)猜想:∠B、∠DAE、∠EAC三个角之间的关系,并加以证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某长途汽车客运公司规定:旅客可免费带一定重量的行李,如果超过规定重量需要购买行李票,设旅客最多可免费携带30千克的行李,超过30千克后每增加1千克,需购买0.5元的行李票,求行李票y(元)与行李重量x(千克)(x>30)之间的函数关系式,如果某旅客买了12元的行李票,那么他带的行李重多少千克?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市某校开展了以“梦想中国”为主题的摄影大赛,要求参赛学生每人交一件作品.现将
从中挑选的50件参赛作品的成绩(单位:分)统计如下:
等级 | 成绩(用m表示) | 频数 | 频率 |
A | 90≤ m ≤100 | x | 0.08 |
B | 80≤ m <90 | 34 | y |
C | m <80 | 12 | 0.24 |
合计 |
| 50 | 1 |
请根据上表提供的信息,解答下列问题:
(1)表中![]() 的值为_____________,
的值为_____________,![]() 的值为______________;(直接填写结果)
的值为______________;(直接填写结果)
(2)将本次参赛作品获得A等级的学生依次用A1、A2、A3……表示.现该校决定从本次参赛作品获得A等级的学生中,随机抽取两名学生谈谈他们的参赛体会,则恰好抽到学生A1和A2的概率为____________.(直接填写结果)
查看答案和解析>>
科目:初中数学 来源: 题型:
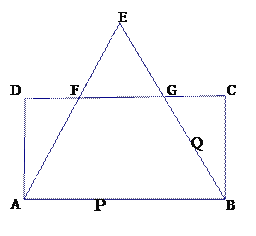
【题目】矩形![]() 中,
中, ![]() ,以
,以![]() 为边向上作正
为边向上作正![]() ,
, ![]() 、
、![]() 分别交
分别交![]() 于
于![]() 、
、![]() ,
, ![]() ,两动点
,两动点![]() 、
、![]() 运动速度分别为4
运动速度分别为4![]() 、
、![]() (
(![]() ).
).
(1)![]() 的长为
的长为 ![]() ;
;
(2)若点![]() 从
从![]() 出发沿线段
出发沿线段![]() 向
向![]() 运动,同时点
运动,同时点![]() 从
从![]() 出发沿线段
出发沿线段![]() 向点
向点![]() 运动,设运动时间为
运动,设运动时间为![]() ,在运动过程中,以
,在运动过程中,以![]() 、
、![]() 、
、![]() 为顶点的三角形和以
为顶点的三角形和以![]() 、
、![]() 、
、![]() 为顶点的三角形全等,求
为顶点的三角形全等,求![]() 的运动速度
的运动速度![]() ;
;
(3)若点![]() 以(2)中的速度从点
以(2)中的速度从点![]() 出发,同时点
出发,同时点![]() 以原来的速度从点
以原来的速度从点![]() 出发,逆时针沿四边形
出发,逆时针沿四边形![]() 运动.问
运动.问![]() 、
、![]() 会不会相遇?若不相遇,说明理由.若相遇,请求出经过多长时间
会不会相遇?若不相遇,说明理由.若相遇,请求出经过多长时间![]() 、
、![]() 第一次在四边形
第一次在四边形![]() 的何处相遇?
的何处相遇?
查看答案和解析>>
科目:初中数学 来源: 题型:
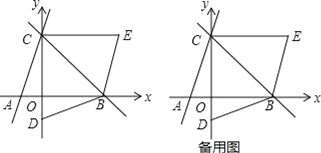
【题目】如图,已知直线y=3x+3与x轴交于点A,与y轴交于点C,过点C的直线y=﹣x+b与x轴交于点B.
(1)b的值为______;
(2)若点D的坐标为(0,﹣1),将△BCD沿直线BC对折后,点D落到第一象限的点E处,求证:四边形ABEC是平行四边形;
(3)在直线BC上是否存在点P,使得以P、A、D、B为顶点的四边形是平行四边形?如果存在,请求出点P的坐标;如果不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com