
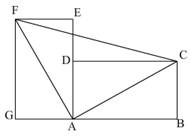
1、 将两个完全相同的长方形拼成如图所示的“L”形图案,判断△ACF是什么三角形?说明理由。
科目:初中数学 来源: 题型:


查看答案和解析>>
科目:初中数学 来源:2013年初中毕业升学考试(河南卷)数学(解析版) 题型:解答题
如图1,将两个完全相同的三角形纸片ABC和DEC重合放置,其中∠C=900,∠B=∠E=300.
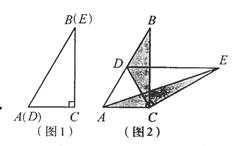

(1)操作发现如图2,固定△ABC,使△DEC绕点C旋转。当点D恰好落在BC边上时,填空:线段DE与AC的位置关系是 ;
②设△BDC的面积为S1,△AEC的面积为S2。则S1与S2的数量关系是 。
(2)猜想论证
当△DEC绕点C旋转到图3所示的位置时,小明猜想(1)中S1与S2的数量关系仍然成立,并尝试分别作出了△BDC和△AEC中BC,CE边上的高,请你证明小明的猜想。
(3)拓展探究
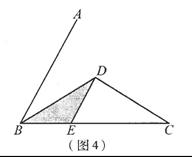
已知∠ABC=600,点D是其角平分线上一点,BD=CD=4,OE∥AB交BC于点E(如图4),若在射线BA上存在点F,使S△DCF =S△BDC,请直接写出相应的BF的长
查看答案和解析>>
科目:初中数学 来源:河北省模拟题 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com